我将2020秋季Berkeley的CS 61A作业发布在我的Github仓库,由于学校课程要求,设置为私人仓库。
几类递归问题:
从给定的数字序列中筛选出符合题意的数字组合,此类题目一般使用Tree Recursion解决,分为使用最后一位数字和不使用最后一位数字两种情况(n //10 & n % 10),这类题目也常依托于列表或者字符串等基础数据结构,但基本的思路是一样的,是比较典型的Tree Recursion问题
此类问题会通过一个变量或者函数参数保存先前遍历过或者查看过的某个变量,在下一次递归中参与比较
此类问题的解决依靠设计嵌套函数,并辅之以跟踪变量index或者某种flag,减小递归难度,如果我们发现在实现过程中,增添一个跟踪指标或者将函数中的某部分独立出来更加方便,则可以考虑使用
这是一类比较特殊的递归问题,使用yield可以帮助我们在这类题目中大大简洁代码,这是因为yield每次生成的generator都会被保存至下一次递归中,而不会随着程序运行结束而消失,从而避免了使用list等数据结构存储或跟随递归生成变量的需要
这一类问题已经被专门整理到一起
HW1
Q2
问题转化的想法:选出两个最大的数,并计算其平方和,其实也就是在计算最大的数值平方组合
max(a*a+b*b,b*b+c*c,a*a+c*c)
Q3
摒弃遍历顺序正序的想法,在此题目中,倒序遍历是最方便的:
factor = n - 1
while factor < n:
if n % factor == 0:
return factor
factor -= 1
Q4
if_function(cond(), true_func(), false_func()中,会先执行其中的函数,之后将其返回值传入主函数。所以执行的过程一定是true_func()->false_func(),执行结果根据提示分别为42与47,又因为statement函数执行结果仅为47,所以一定是true_func()对应47,那么false_func()对应42,根据之前的执行顺序,条件判断函数cond()应当设定为false。
if cond():
return true_func()
else:
return false_func()
同时把握下图:
整数除法://
Lab1
Veritasiness
>>> 1 and 3 and 10 and 15
>>> 15
执行顺序为自左至右,如果第一项为True,则判定第二项,以此类推!
Coding Practice
努力把代码写的具有被语言本身的特性,看起来更加简洁:
def falling(n, k):
"""Compute the falling factorial of n to depth k."""
total, stop = 1, n-k
while n > stop:
total, n = total*n, n-1
return total
F20 Lecture 4
lambda
定义一个search函数,找到满足条件的x:
def search(f):
x = 0
# 注意这里loop语法简洁
while not f(x):
x += 1
return x
现在我们想要做一个inverse函数,作为反函数求值器,课上给出的解法如下:
def inverse(f):
return lambda y:search(lambda x:f(x)==y)
对于这个问题,我们可以做如下分析:
在search函数中,条件被设定为f(x);而在inverse函数中,我们的目标是通过给出的函数f,可以对任意y值获取满足条件f(x)==y的x。
如果使用lambda操作,很方便的一点是可以借助lambda的匿名特点,表示我们需要的条件。因为我们要求的是反函数中的x,但是又需要引入未知数x,此时如果是通过def的形式引入变量x,就显得冗余,因为在search函数内部还有一个我们会真正用到的x,而匿名函数lambda恰好解决了这一问题。同样地,lambda也可以用于引入参数y。
而如果使用def的形式定义函数,则最方便的办法是先将search函数更改为如下形式:
def search(f, y):
x = 0
# 注意这里loop语法简洁
while not f(x) == y:
x += 1
return x
inverse函数做如下定义:
def inverse(f):
def SetY(y):
return search(f, y)
return SetY
如果我们选择不更改search函数,则inverse函数:
def inverse(f):
def SetY(y):
# 因为只有在这个frame里才需要用到x,所以选择在另一个函数内部定义SetX,其实是和匿名函数一个道理
def SetX(x):
return f(x) == y
return search(SetX)
return SetY
这里要学习的还有从特例到抽象的推导思维,这有助于我们快速构建出程序结构。先从开平方根函数的特例开始:
# 一个平方查找函数
def is_square_of_4(n):
return square(4) == n
# 一个平方根查找函数
def is_sqrt_of_16(x):
return square(x) == 16
# 利用search函数寻找x:
ans = search(is_sqrt_of_16)
# 扩充使用案例到16->n:
def sqrt(n):
def is_sqrt_of_n(x):
return square(x) == n
return search(is_sqrt_of_n)
# 扩充平方根函数,设计inverse,从内向外,逐层添加:
def inverse(f):
def is_inverse_of_f(y):
def is_inverse_of_y(x):
return f(x) == y
return search(is_inverse_of_y)
return is_inverse_of_f
调用函数:
# e.g.
sqrt = inverse(square)
Ans = sqrt(256)
这里的256就是函数中的y参数,这也是为什么要把return写做lambda y:...的原因,我们要先给到参数y。
call expression中的执行顺序
为什么不会出现if_(c,t,f)这种形式?因为这是一个call expression (which applies a function to some arguments),而根据如下的evaluation规则,这种函数设计很容易出现问题,所有子表达式均要提前被执行:

Hog(Higher Order Function)
Q8 Test
>» dice = make_test_dice(3, 1, 5, 6)
>» averaged_roll_dice = make_averaged(roll_dice, 1000)
>» # Average of calling roll_dice 1000 times
>» # Enter a float (e.g. 1.0) instead of an integer
>» averaged_roll_dice(2, dice)
最终的结果为6.0。其中部分函数如下:
def make_test_dice(*outcomes):
"""Return a die that cycles deterministically through OUTCOMES.
>>> dice = make_test_dice(1, 2, 3)
>>> dice()
1
>>> dice()
2
>>> dice()
3
>>> dice()
1
>>> dice()
2
This function uses Python syntax/techniques not yet covered in this course.
The best way to understand it is by reading the documentation and examples.
"""
assert len(outcomes) > 0, 'You must supply outcomes to make_test_dice'
for o in outcomes:
assert type(o) == int and o >= 1, 'Outcome is not a positive integer'
index = len(outcomes) - 1
def dice():
nonlocal index
index = (index + 1) % len(outcomes)
return outcomes[index]
return dice
def roll_dice(num_rolls, dice=six_sided):
"""Simulate rolling the DICE exactly NUM_ROLLS > 0 times. Return the sum of
the outcomes unless any of the outcomes is 1. In that case, return 1.
num_rolls: The number of dice rolls that will be made.
dice: A function that simulates a single dice roll outcome.
"""
# These assert statements ensure that num_rolls is a positive integer.
assert type(num_rolls) == int, 'num_rolls must be an integer.'
assert num_rolls > 0, 'Must roll at least once.'
i, sum = 0, 0
flag_1 = False
while i < num_rolls:
res = dice()
if res == 1:
flag_1 = True
else:
sum += res
i += 1
if flag_1:
sum = 1
return sum
这要涉及到的知识点是Higher Order Function,以及一个nonlocal关键字。需要注意的是,只要[f1=make_test_dice]这个frame没有变,也就是说我们没有在另一个[f2=make_test_dice]里操作,那么无论我们执行多少次dice(*args),变量index的值始终是循环的,因为根据environment diagram的原则,它的作用域f1没有消失。
Q7
在Problem 7提供的样例中,有几个有趣的Higher Order Function:
def say_scores(score0, score1):
"""A commentary function that announces the score for each player."""
print("Player 0 now has", score0, "and Player 1 now has", score1)
return say_scores
def announce_lead_changes(last_leader=None):
"""Return a commentary function that announces lead changes."""
>>> f0 = announce_lead_changes()
>>> f1 = f0(5, 0)
Player 0 takes the lead by 5
>>> f2 = f1(5, 12)
Player 1 takes the lead by 7
>>> f3 = f2(8, 12)
>>> f4 = f3(8, 13)
>>> f5 = f4(15, 13)
Player 0 takes the lead by 2
def say(score0, score1):
if score0 > score1:
leader = 0
elif score1 > score0:
leader = 1
else:
leader = None
if leader != None and leader != last_leader:
print('Player', leader, 'takes the lead by', abs(score0 - score1))
return announce_lead_changes(leader)
return say
其中的say函数,返回值为announce_lead_changes(leader),因为这是一个call expression,所以会重新建立一个environment diagram,其中的formal parameter由刚执行完毕的say函数给出,并作为即将执行的announce_lead_changes的参数,又传入以它为parent的say函数中使用。
def both(f, g):
"""Return a commentary function that says what f says, then what g says."""
NOTE: the following game is not possible under the rules, it's just
an example for the sake of the doctest
>>> h0 = both(say_scores, announce_lead_changes())
>>> h1 = h0(10, 0)
Player 0 now has 10 and Player 1 now has 0
Player 0 takes the lead by 10
>>> h2 = h1(10, 8)
Player 0 now has 10 and Player 1 now has 8
>>> h3 = h2(10, 17)
Player 0 now has 10 and Player 1 now has 17
Player 1 takes the lead by 7
def say(score0, score1):
return both(f(score0, score1), g(score0, score1))
return say
母函数返回子函数的同时,子函数返回母函数–这样做的好处在于一直跟随leader的变化,同时可以连续使用(score0,score1)的格式。在CS 61A提供的文档中,表明这是commentary function的常用写法(即利用Higher Order Function).

Disc 02(Higher Order Function)
一道很有趣的HOF题目:
y = "y"
h = y
def y(y):
h = "h"
if y == h:
return y + "i"
y = lambda y: y(h)
return lambda h: y(h)
y = y(y)(y)

进行变量查找时,先在该作用域内查找对应的变量名称和值,如果找不到,进入其parent frame中查找,依此递推。所以在程序段最后调用y时,它所指向的应该是global frame中的func y(y),而不是func y(y) frame中的return lambda h: y(h)中的y则是来自于本frame中的y = lambda y: y(h).
F20 Lecture 8(Recursion)
主要围绕递归进行讨论:
递归的主要原则就是通过函数的递归,逐步将原始问题转化为更简单的问题,最终将问题定位到base case上,递归结束,并给之前使用的函数逐个提供返回值。
递归的依据是数学归纳法,即在证明(或者说给出)k=1和k=n-1的解法之后,即可证明(推断出)k=n的情况。我们也可以依据这一原则验证我们写出的递归函数是否正确,即分别验证k=1的情况,并假定k=n-1的情况是正确的,观察我么能否得到需要的k=n的结果。
在写递归函数时,不要尝试推导递归过程,尝试用抽象思维定义函数。
mutual recursion
此种情况适用于单一递归函数解决起来比较繁琐,或者不适于解决的问题:
e.g. 银行卡号计算问题:
def sum_digits(n):
if n < 10:
return n
else:
all_but_last, last = n // 10, n % 10
return sum_digits(all_but_last) + last
def luhn_sum(n):
if n < 10:
return n
else:
all_but_last, last = n // 10, n % 10
return luhn_sum_double(all_but_last) + last
def luhn_sum_double(n):
all_but_last, last = n // 10, n % 10
last = sum_digits(2*last)
if n < 10:
return last
else:
return luhn_sum(all_but_last)+last
这里的mutual recursion实质上是针对奇偶两种情况的讨论,而也正因为如此,我们可以将两个函数合并到一个函数内来写:
def luhn_sum(n, i=1):
if n < 10:
return sum_digits(2*n) if i % 2 == 1 else n
else:
all_but_last, last = n // 10, n % 10
if i % 2 == 1:
i += 1
return luhn_sum(all_but_last, i) + last
else:
i += 1
last = sum_digits(2*last)
return luhn_sum(all_but_last, i) + last
只要设置一个奇偶指示标志即可。
trick
遇到复杂的递归问题如何解决?我们要设想在问题解决的前一步乃至前几步的变化,比如汉诺塔问题,我们正是借助于对k=n-1的情况的了解,进行参数变换,并将k=n的问题成功转化为三个步骤。再比如这个问题:
n个自然数中取出r个数字的组合
首先我们举例:654321,6选4,我们可以将问题分为如下几种情况:
- 固定6,问题转化为从54321这5个数字中选3个数
- 固定5,问题转化为从4321这4个数字中选3个数(无6)
- 固定4,问题转化为从321这3个数字中选3个数(无56)
一开始的思路是想把这四步写成递归,但是发现存在问题:这几步是分别独立的步骤,我们无法在递归程序中先固定6,之后又不考虑6,也就是说不可能按照时间顺序先后发生。
于是,我们将上边的情况1的后续步骤写出来:
固定6,问题转化为从54321这5个数字中选3个数->固定4(已有64),问题转化为从5321这4个数字中选2个数->固定3(已有456),问题转化为从521这3个数字中选1个数……
这个步骤,是可以写作递归的!于是前边的几种情况,我们可以考虑写成循环(iteration).(这也符合将递归变成一个simpler question的准则,转化后的问题又是一个可以写成一个有iteration的,可以继续分解的子问题…)
于是我们接下来思考,递归的base case是什么?通过上边的案例,不难发现是r=1。在base case时,要做什么?就是把之前已经被固定(选择好的)数字输出,为了达到这一目的,我们将之前遍历过的数字用数字保存起来。
a = []
for i in range(100):
a.append(0)
def list_r_from_n(n,r):
for i in range(n,r-1,-1):
# 保存遍历过的数字
a[r]=i
# base case:
if r == 1:
for j in range(a[0],0,-1):
print(a[j])
print(end='\n')
# 不可以a.clear()
else:
list_r_from_n(n - 1, r - 1)
a[0]=r
注意在保存遍历过的数字时,不要使用a.append(i)和a.clear()的方式,因为最外层的循环并非仅仅会经历n-r+1次,直接清空整个列表会导致排在前边的数据缺失。
此外,递归也可以运用在higher order function中,如:
def repeat(i):
if i == 0:
return x
else:
return f(repeat(i - 1))
return repeat
Tree recursion
Order of Recursive Calls

Tree Recursion分析方法
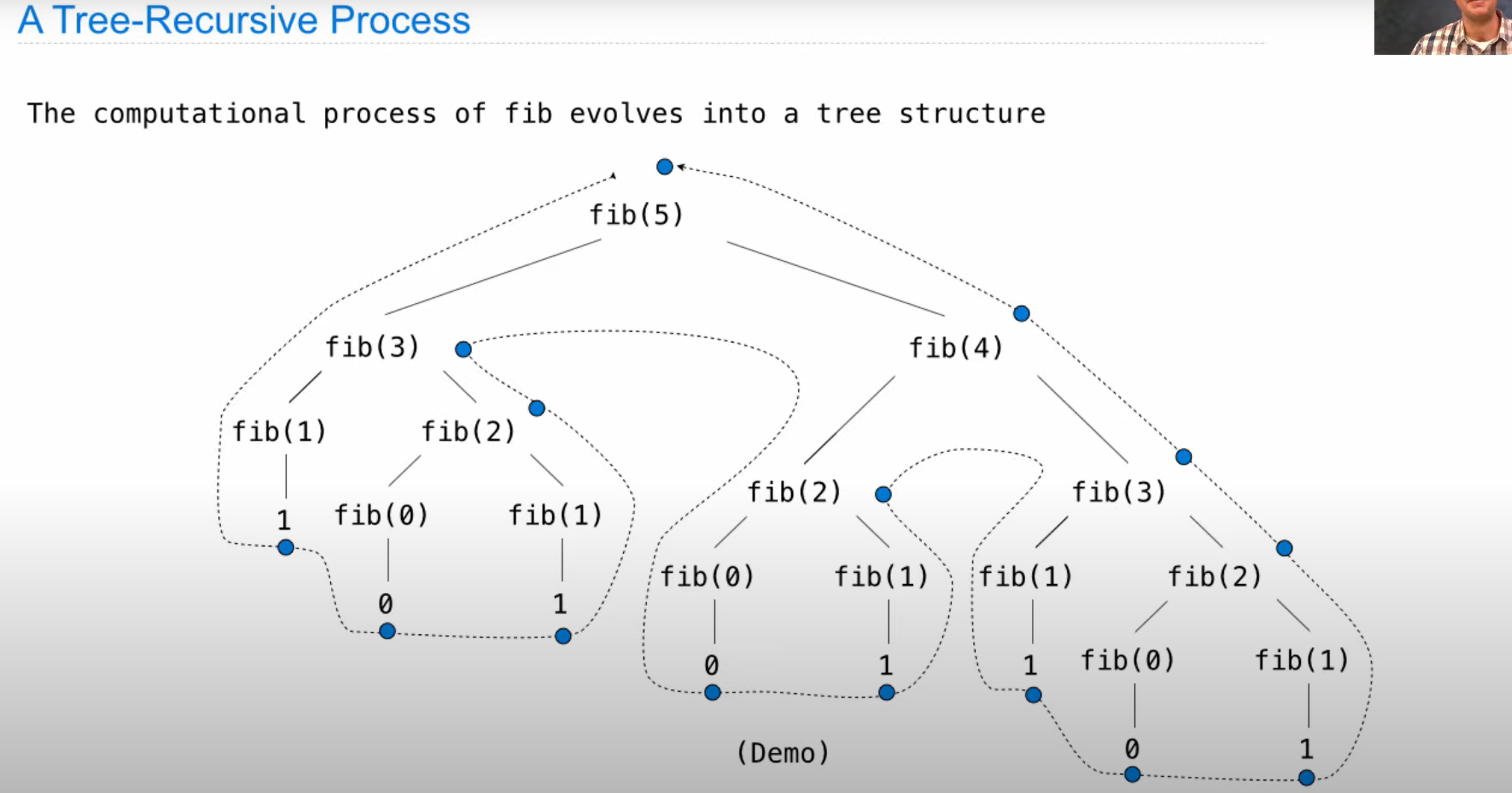
解决Tree recursion的基本方法是进行recursive decomposition,尝试找到问题更简单的案例。比如Counting Partitions的例子,考虑count_partitions(6,4)就可以分解为两个子问题:
- 至少有一个4->count_partitions(2,4)
- 不使用4->count_partitions(6,3)
之后再将例子拓展即可:
with_m = count_partitions(n-m,m)
without_m = count_partitions(n,m-1)
return with_m + without_m
Number Selection Problem
从给定的一个长整数中选出满足题意的数字组合,一般使用Tree recursion方法解决:
根据Tree recursion的方法,可以写出问题trick的另一种解法:
trick1
n个自然数中取出r个数字的组合
的另一种解法:
将问题list_r_from_n(6,4)划分为两个子问题:
- 数字组合中不包含6->list_r_from_n(5,4)
- 数字组合中至少包含一个6->list_r_from_n(5,3)
将例子拓展:
def list_r_from_n(n, r):
if r == 0:
for j in range(a[0], 0, -1):
print(a[j], end='')
print(end='\n')
return 0
if n < r:
return 0
else:
# 进入else,先把正在讨论的数固定住
a[r] = n
list_r_from_n(n - 1, r - 1)
list_r_from_n(n - 1, r)
a[0] = r
类似的例子还出现在lab04和disc04当中:
Lab 04
def max_subseq(n, t):
"""Return the maximum subsequence of length at most t that can be found in the given number n."""
if t == 0:
return 0
if n // 10 == 0:
return n
else:
all_but_last, last = n // 10, n % 10
return max(max_subseq(all_but_last, t - 1) * 10 + last, max_subseq(all_but_last, t))
还是用之前的思路分析一遍问题:
假设n为34521,t为3,问题可以分为两种情况:
- 3个数的子序列中,不使用n的最后一个数字:则n为3452,t为3
- 3个数的子序列中,使用n的最后一个数字:则n为3452,t为2,之后使用
10*n+d的方法将末位固定住,这里相当于假设max_subseq(all_but_last,t-1)会返回正确的东西(数学归纳法)
将1与2得到的数字比较大小
用yield如何解决Number Selection Problem?
本题目来自于spring 2020 midterm2
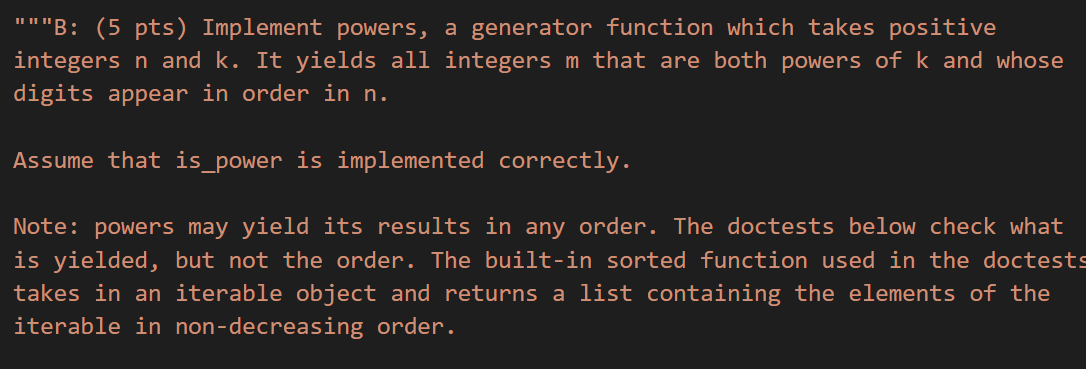
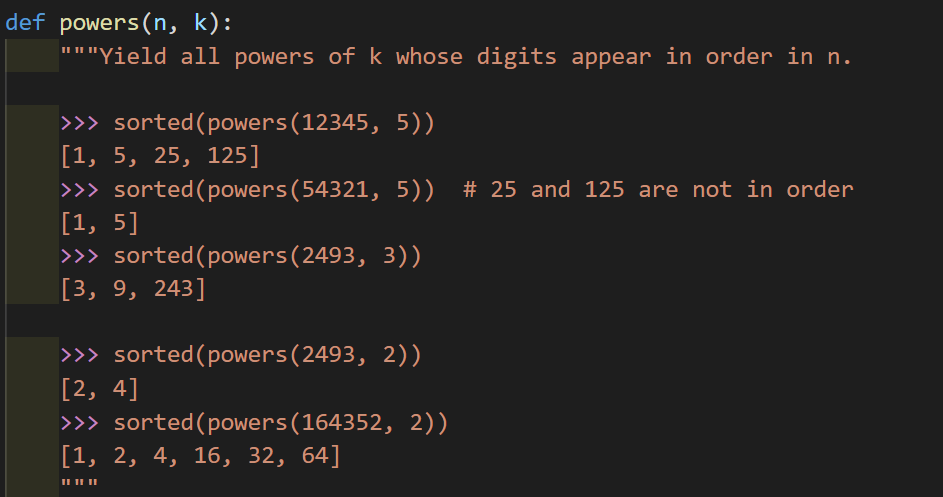
curry2 = lambda f: lambda x: lambda y: f(x, y)
def powers(n, k):
"""Yield all powers of k whose digits appear in order in n."""
def build(seed):
"""Yield all non-negative integers whose digits appear in order in seed.
0 is yielded because 0 has no digits, so all its digits are in seed.
"""
if seed == 0:
yield 0
else:
for x in build(seed // 10):
yield x
yield x * 10 + seed % 10
yield from filter(curry2(is_power)(k), build(n))
这道题目的总体思路是先把所有数字组合排列出来,之后再利用先前实现的is_power函数把符合题意的数字组合筛选出来。注意到在build函数内部的数字组合方法,与上边的lab 04十分相似,其实也是假定(数学归纳法)build(seed//10)这个更简单的递归问题返回正确的数字组合,之后把末尾数字考虑进去。
disc 04

或者,当问题不再能简单的二分时,我们可以通过循环的方式统计所有可能性:


sp18-final 5 (b)

这道题的关键在于要首先发现是一个Tree Recursion的问题,当k为因数时,我们可以选择使用或者不使用,从而对应了Tree Recursion的两种情况:
def factorize(n, k=2):
if n == k:
return 1
elif n < k:
return 0
elif n % k != 0:
return factorize(n, k + 1)
return sum([factorize(n // k, k), factorize(n, k + 1)])
Summer 2020 Practice mt Q3
这是一道更为复杂的Number selection Problem,题目要求如下:

我们可以从一个更简单的Number selection Problem入手,即省略掉上面题目中数字递增顺序可以从i+2位开始的要求,要求全部递增,则我们可以完成如下的函数设计:
def increasing(n, smallest=10):
if n == 0:
return 0
# 意味着可以使用当前的末位数字
no = increasing(n // 10, smallest)
if n % 10 < smallest:
# 现在最小的数字变成了n%10
yes = increasing(n // 10, n % 10) * 10 + n % 10
return max(no, yes)
else:
return no
那么在此题中,因为递增数字序列中间可以间隔一个数字,所以我们思考是否有办法将最小值的比较和确定滞后一位,使得smallest代表隔一位数字后的最小值。也就是说当我们面对435时,如果要插入4,此时我们想要比较的对象(名义最小值)为5,而非前一步刚加入的3。所以题目尝试加入一个参数d,用以保存当前轮次的末尾数字,并将该末位数字d在下一轮加入最小值smallest的比较。这样一来,smallest中存储的就是隔一位之后的数字最小值了:
def cloase(n, smallest=10,d=10):
if n == 0:
return 0
no = close(n, smallest,d)
if n % 10 < smallest:
yes = close(n // 10, min(smallest, d), n % 10) * 10 + n % 10
return max(yes, no)
return no
长度最长的数字,也就意味着数值最大的数字,在解法中,运用了这个关系
HW2 (Recursion+Higher Order Function)
在对应的HW中,给出了将Tree Recursion与Higher Order Function相结合的例子.
同时注意在使用递归时,如果我们有多个数据需要追踪,可以写一个helper函数:
def count_coins(total):
"""Return the number of ways to make change for total using coins of value of 1"""
def count_helper(total, m):
if total == 0:
return 1
elif total < 0:
return 0
elif m is None:
return 0
elif total < m:
return 0
else:
return count_helper(total - m, m) + count_helper(total, next_largest_coin(m))
return count_helper(total, 1)
这也是一个tree recursion问题,根据处理这类问题的方法,我们尝试寻找一个标准,将问题分为几个更简单的instance。依靠helper函数,问题转化为:
- 不用当前最小面值硬币1,则问题转化为使用最小面值硬币
next_largest_coin(1),凑齐总价值total - 至少使用一个面值为1的硬币,则问题转化为使用最小面值硬币1,凑齐总价值为
total-1
我们将分析写成函数,就是上边的形式。
def pingpong(n):
"""Return the nth element of the ping-pong sequence."""
if n <= 8:
return n
else:
return pingpong(n - 1) + helper(n - 1)
# 决定是要+1还是-1
def helper(n):
if n <= 7:
return 1
else:
if n % 8 == 0 or num_eights(n) != 0:
return -helper(n - 1)
else:
return helper(n - 1)
使用lambda函数,在不给出函数名的情况下定义递归:
>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1)))
>>> fact(5)
120
def make_anonymous_factorial():
"""Return the value of an expression that computes factorial."""
return (lambda f: lambda n: f(f,n))(lambda s,x: 1 if x == 1 else mul(x, s(s,sub(x, 1))))
这里理解的点在于,递归的过程实质上是把函数本身也作为了函数的参数,在函数内部调用了函数自己.
F20 Lecture 10(List)
- list的concatenation & repetition
# 将原来的所有元素重复一遍并加上[2,7]元素
[2,7]+lists*2
- Sequence Unpacking
pairs = [[1,2],[2,2],[3,4]]
for x,y in pairs:
if x == y:
...
- list constructor
list(range(4))
List / String 在Tree Recursion中的使用
cats
Problem 7 (3 pt)
Implement
pawssible_patches, which is a diff function that returns the minimum number of edit operations needed to transform thestartword into thegoalword.There are three kinds of edit operations:
- Add a letter to
start,- Remove a letter from
start,- Substitute a letter in
startfor another.Each edit operation contributes 1 to the difference between two words.
>>> big_limit = 10 >>> pawssible_patches("cats", "scat", big_limit) # cats -> scats -> scat 2 >>> pawssible_patches("purng", "purring", big_limit) # purng -> purrng -> purring 2 >>> pawssible_patches("ckiteus", "kittens", big_limit) # ckiteus -> kiteus -> kitteus -> kittens 3We have provided a template of an implementation in
cats.py. This is a recursive function with three recursive calls. One of these recursive calls will be similar to the recursive call inshifty_shifts.You may modify the template however you want or delete it entirely.
If the number of edits required is greater than
limit, thenpawssible_patchesshould return any number larger thanlimitand should minimize the amount of computation needed to do so.>>> limit = 2 >>> pawssible_patches("ckiteus", "kittens", limit) > limit True >>> pawssible_patches("ckiteusabcdefghijklm", "kittensnopqrstuvwxyz", limit) > limit True
def pawssible_patches(start, goal, limit):
"""A diff function that computes the edit distance from START to GOAL."""
if limit < 0:
return 0
if start == '':
return len(goal)
elif goal == '':
return len(start)
elif start[0] == goal[0]:
return pawssible_patches(start[1:], goal[1:],limit)
else:
limit -= 1
add_diff = pawssible_patches(goal[0] + start, goal,limit)
remove_diff = pawssible_patches(start[1:], goal,limit)
substitute_diff = pawssible_patches(goal[0] + start[1:], goal,limit)
return 1 + min(add_diff, remove_diff, substitute_diff)
对于这道问题,我们可以类比之前的Tree Recursion递归问题,思考如何把问题抽象化:
对于每一个位置的字符对比,都有增删改三种操作,可以联想之前爬楼梯的问题:每一步都有上1级台阶或者2级台阶这两种情况,只是在这里,增删改这三种操作不简单的是f(n-1)这种形式,我们需要自己实现它。所以现在基本可以确定,递归会作用在实现增删改这三种操作上,接下来要完善函数设计,就要思考如下几个问题:
- base case是什么?
首先刨除limit这个变量不管,显然在我们在递归至字符串start或者goal任意一个为空字符串时,递归停止,并返回另一字符串的长度(及需要进行改变的次数)
- 如何进行
recursion decomposition?
起点很简单,一定是字符串开头的首字母,所以可以分为首字母相同与首字母不同两种情况,如果首字母相同,就不需要利用增删改三者当中的任何一个,那么这个simpler instance可以写作:
elif start[0] == goal[0]:
return pawssible_patches(start[1:], goal[1:],limit)
如果首字母不相同,这时候就需要进行增删改的操作,但要注意,我们将goal的首位递推的任务交给两者相同的情况,以免发生错误。只要进行了一次更改操作,次数要加1,所又因为题目要求计算最小更改次数,所以每一次,我们都选取这三种操作里需要次数最少的那一个并随之递归:
else:
limit -= 1
add_diff = pawssible_patches(goal[0] + start, goal,limit)
remove_diff = pawssible_patches(start[1:], goal,limit)
substitute_diff = pawssible_patches(goal[0] + start[1:], goal,limit)
return 1 + min(add_diff, remove_diff, substitute_diff)
最后,为了提高程序运行的效率,我们需要计算何时达到limit,于是在每一次更改之后,都将limit减小1,在limit达到0时,停止递归。
Lab 14 Q6
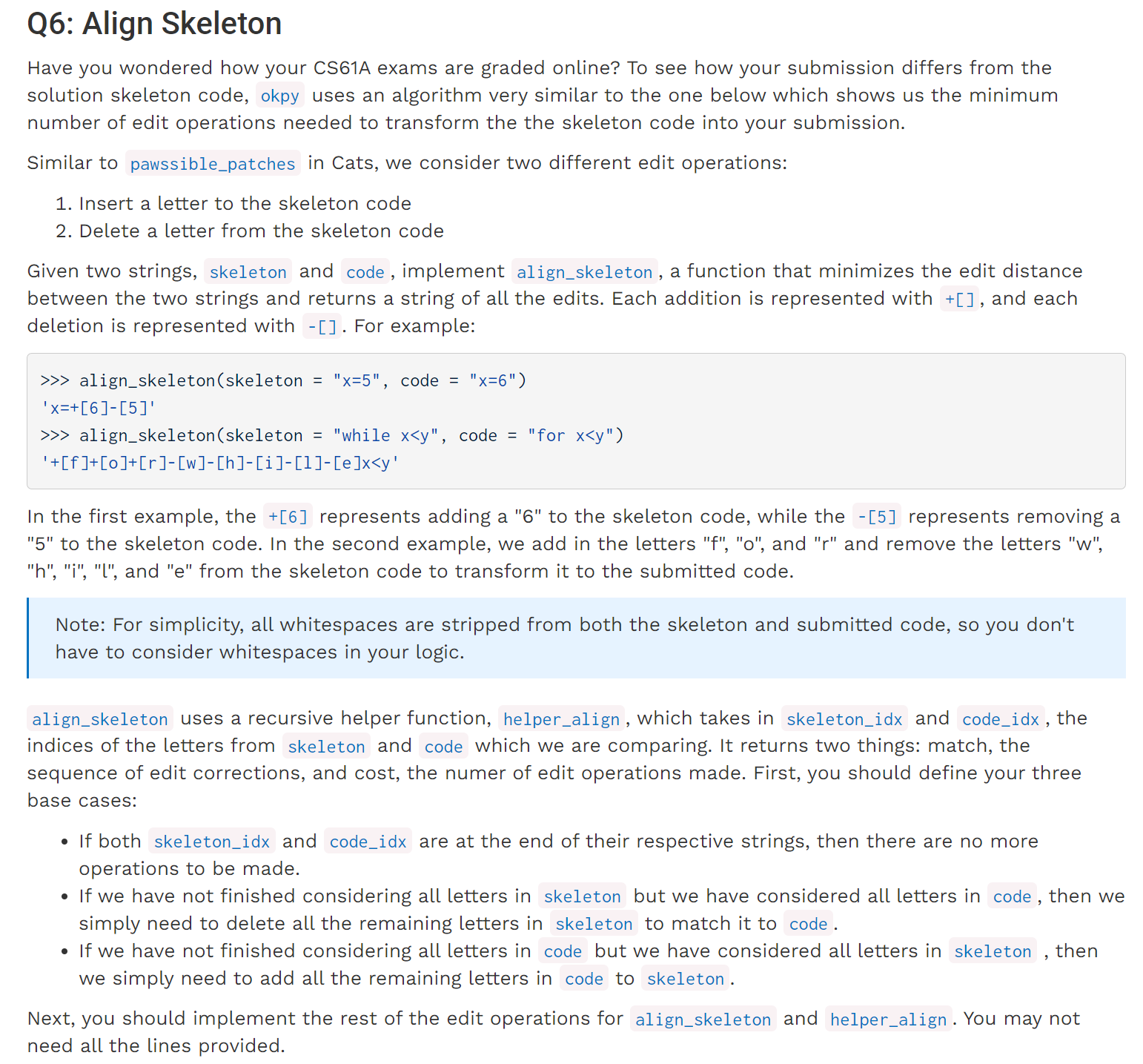
这道题题目很长,但是给出了不少的template,在这里我们直接抛弃template,看整体的实现思路是怎样的:
def align_skeleton(skeleton, code):
"""Aligns the given skeleton with the given code, minimizing the edit distance between the two."""
skeleton, code = skeleton.replace(" ", ""), code.replace(" ", "")
def helper_align(skeleton_idx, code_idx):
"""
Aligns the given skeletal segment with the code.
Returns (match, cost)
match: the sequence of corrections as a string
cost: the cost of the corrections, in edits
"""
# 位于末尾且匹配
if skeleton_idx == len(skeleton) and code_idx == len(code):
return '', 0
# 位于末尾且需要删除
if skeleton_idx < len(skeleton) and code_idx == len(code):
edits = "".join(["-[" + c + "]" for c in skeleton[skeleton_idx:]])
return edits, len(skeleton) - skeleton_idx
# 位于末尾且需要增加
if skeleton_idx == len(skeleton) and code_idx < len(code):
edits = "".join(["+[" + c + "]" for c in code[code_idx:]])
return edits, len(code) - code_idx
possibilities = []
skel_char, code_char = skeleton[skeleton_idx], code[code_idx]
# Match
if skel_char == code_char:
result, cost = helper_align(skeleton_idx + 1, code_idx + 1)
new_result = skel_char + result
possibilities.append((new_result, cost))
# Insert
result1, cost1 = helper_align(skeleton_idx, code_idx + 1)
new_result1 = "+[" + code_char + "]" + result1
possibilities.append((new_result1, 1 + cost1))
# Delete
result2, cost2 = helper_align(skeleton_idx + 1, code_idx)
new_result2 = "-[" + skel_char + "]" + result2
possibilities.append((new_result2, 1 + cost2))
# 返回操作次数最少的情况
return min(possibilities, key=lambda x: x[1])
result, cost = helper_align(0, 0)
return result
在题目的叙述中,其实已经给出了不少提示,在这里我们需要注意以下几点:
- 当一个序列达到末尾,但是另一个没有时,我们需要返回对应的编辑操作以及长度,但是注意这里的长度并非
len(edits),而是余下的原序列的字符长度,不包括增加的[]等。 - 在考虑了三种
base case之后,是递归的主体部分。在原题目给出的template中有一个数组possibilities,我们应当首先思考这个数组的作用,或者说当自己解题时,也要借助于这种方法实现此类问题:利用该数组得到当前某一步(比如第(n-1)步)所有的操作序列,并对应的操作数最少的那种,传递给需要处理的第n个字符。一般这种操作都是先把所有情况存储起来(Delete/Insert),最后在return处使用min/max进行选择。 - 当时在解这道题时,主要卡在了
Match的情况,原本想对两个flag分别增加,但是发现这样处理之后insert/Delete的情况可能会出现溢出,所以换一种思路:直接在Match内部递归一次函数,把flag的增加直接体现在函数参数上
F20 Lecture 21 Q&A

def decrypt(s, d):
# base case 1:
if s == '':
return []
ms = []
# base case 2:
if s in d:
ms.append(d[s])
# recursive case, make sure that at least 1 char at the front and the end:
for k in range(1, len(d) - 1):
first, suffix = s[:k], s[k:]
if first in d:
for rest in decrypt(suffix,d):
ms.append(d[first] + ' ' + rest)
return ms
lab 09
subseqs & inc_subseqs
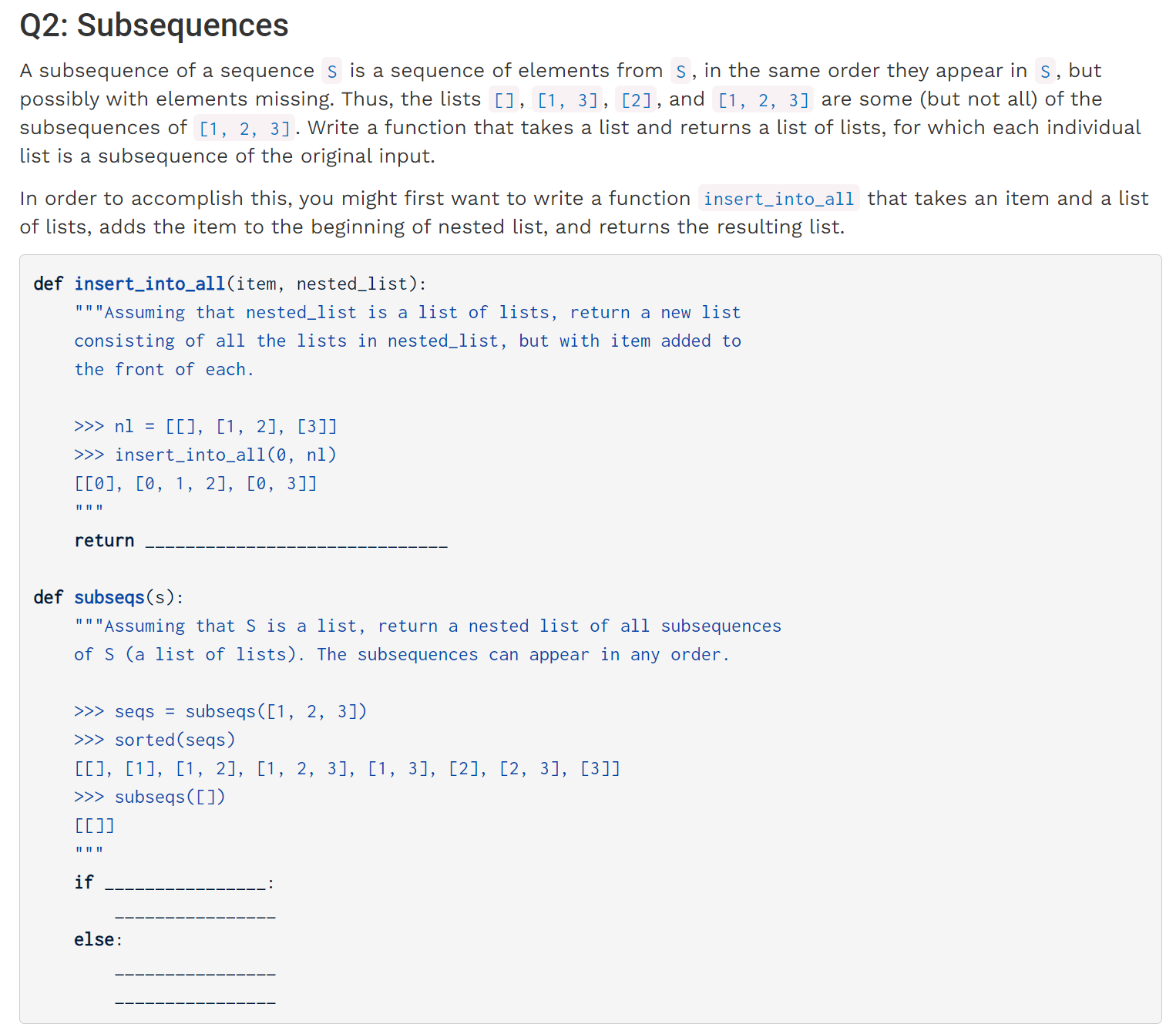
insert_into_all函数较为容易实现:
def insert_into_all(item, nested_list):
return [[item] + elem for elem in nested_list]
而subseqs是一个比较典型的Number Selection problem with lists,只不过这次是从头部开始的,面对这种问题,我们可以先考察s[1:]时的情况,以[2,3]为例,那么此时的返回值应当为[[],[2],[3],[2,3]],于是我们可以发现规律,当我们试图把问题从s[1:]转化到s时,其实是在s[1:]结果的基础上在第一位插入s[0]。于是借助于之前实现的函数,不难写出:
def subseqs(s):
if not s:
return [[]]
else:
return insert_into_all(s[0], subseqs(s[1:])) + subseqs(s[1:])
在该函数的基础上,题目要求我们实现:
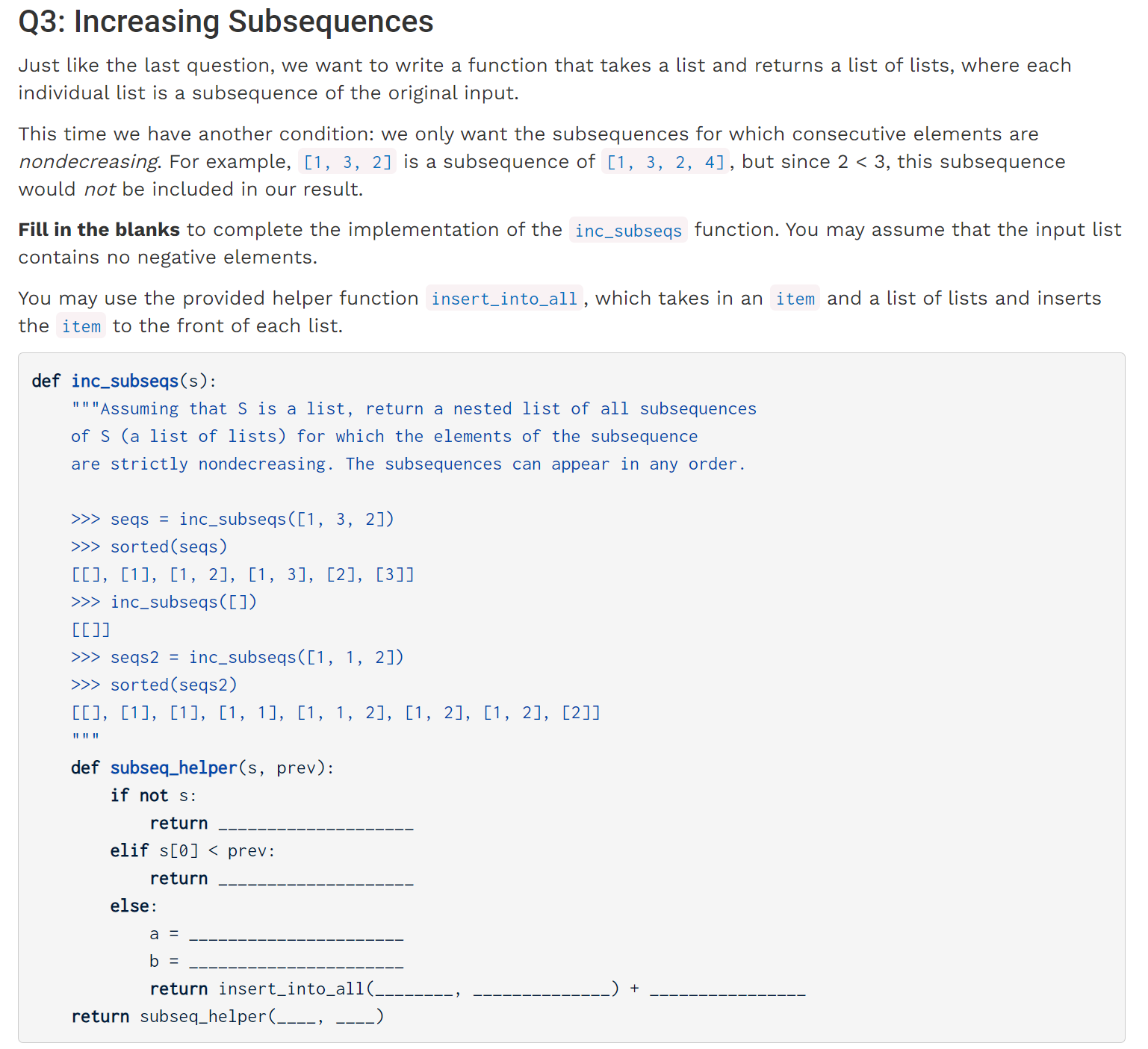
这道题目有点类似于Summer 2020 Practice mt Q3,设立一个prev变量用于保存先前遍历过的数字,也就是上一次递归中(如果列表被改变)的起始位。
我们可以这样思考:当我们尝试将3与组合[2,4]放到一起时,[3,2]不可以出现,因为此时的prev,3要比s[0],2大。因为我们是从前向后遍历的,按照Tree recursion的方法,加入此时我们决定选用3,那么意味着2是不可以被使用的,则下边应继续比较的对象就为s[1:]了:
def inc_subseqs(s):
def subseq_helper(s, prev):
if not s:
return [[]]
elif s[0] < prev:
return subseq_helper(s[1:], prev)
else:
# 用s[0],那么需要更新prev的值为s[0]
a = subseq_helper(s[1:], s[0])
# 不用s[0]
b = subseq_helper(s[1:], prev)
return insert_into_all(s[0], a) + b
return subseq_helper(s, 0)
Lab 14 Q4
这道题当时被卡住,主要是因为没有想到如何将问题转化为可以用程序语言描述的Tree Recursion问题。
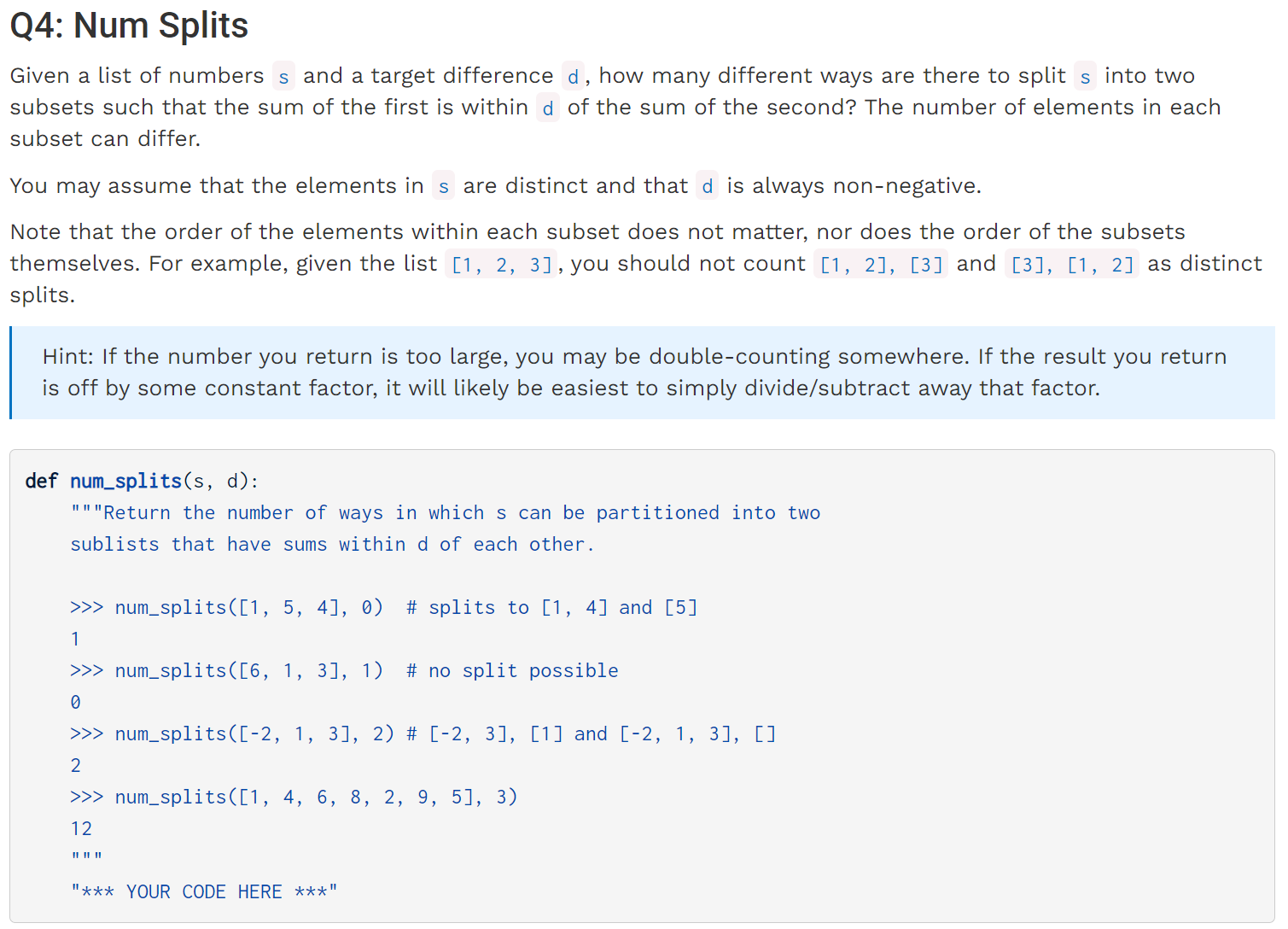
对于某个数字,我们可以选择加入前半个子集,也可以选择不加入,问题的转化关键就在于,当我们选择放弃某个数字时,其实就默认了要将该数字放在后半个子集里。如此一来,题目中要求的difference也会发生对应的+-变化,形成了Tree Recursion:
def num_splits(s, d):
def difference_so_far(s, difference):
if not s:
if abs(difference) <= d:
return 1
return 0
element = s[0]
s = s[1:]
return difference_so_far(s, difference + element) + difference_so_far(s, difference - element)
return difference_so_far(s, 0) // 2
注意到上述的计算过程其实是恰好重复计算了一遍,所以结果要除以2.
注意灵活处理返回值
disc 14

这道题思路不难,但是需要注意当我们发现无法通过对前序代码下手得到需要的结果时,可以考虑在return值上做变换处理。
def paths(x, y):
if x > y:
return []
elif x == y:
return [[x]]
else:
a = paths(x + 1, y)
b = paths(x * 2, y)
return [[x] + subpath for subpath in a + b]
F20 Lecture 12(Recursion->Tree)
详细阐述了如何使用递归完成关于树的各种操作,以及一些container的相关操作。
sum(iterable[,start])->value
>>> sum([[2,3],[4]],[])
[2,3,4]
max(iterable[,key=func])->valueall(iterable)->bool
Return True if bool(x) is True for all values in x in the iterable. If the iterable is empty, return True.
Tree
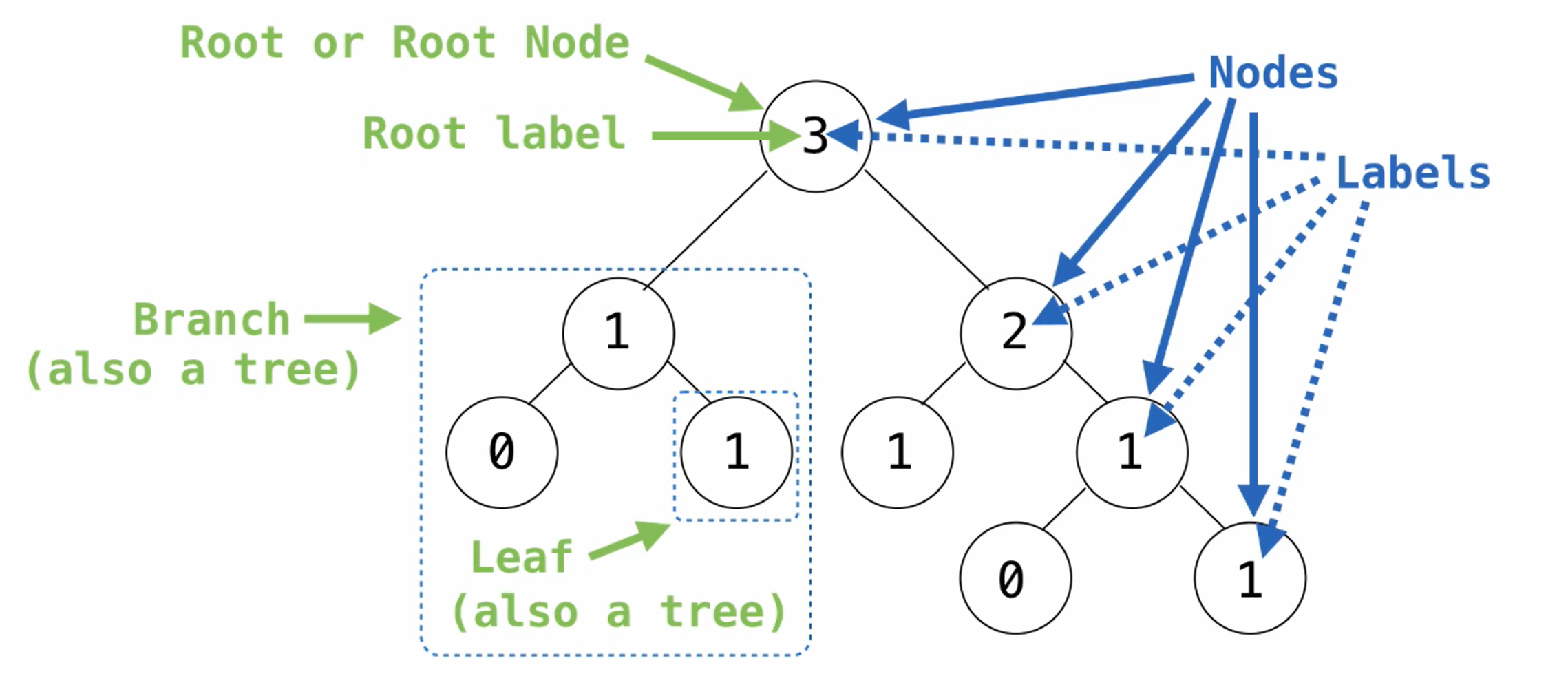
如何构造一个树?
e.g.
>>> tree(3,[tree(1),tree(2,[tree(1),tree(1)])])
[3,[1],[2,[1],[1]]]
定义如下几个函数:
def tree(label, branches=[]):
return [label] + branches
def label(tree):
return tree[0]
def branches(tree):
return tree[1:]
def is_tree(tree):
if type(tree) != list or len(tree) < 1:
return False
for branch in branches(tree):
# 这里的条件判断语句是有必要的,如果我们单单进行循环的话,最后势必会回到函数最下端的返回值那里,那判断也就失去了意义,通过if条件,程序在某一时刻直接结束
if not is_tree(branch):
return False
return True
def is_leaf(tree):
# 判断是否为empty
return not branches(tree)
利用这几个基本的函数,可以处理一些更为具体的Tree Porcessing,比如构造一个Fibonacci树:
def fib_tree(n):
if n <= 1:
return tree(n)
else:
left, right = fib_tree(n-1), fib_tree(n-2)
return tree(label(left)+label(right),[left,right])
以及一些更高阶的Tree Processing函数,比如对叶(leaves)进行的操作:
def count_leaves(t):
# 判断是否为叶结点,常作为base case
if is_leaf(t):
return 1
else:
branch_counts = [count_leaves(b) for b in branches(t)]
return sum(branch_counts)
def leaves(tree):
'''Return a list containing the leaf labels of tree.'''
if is_leaf(tree):
return [label(tree)]
else:
# 利用sum()函数对list操作的特殊性质,每次return遇到sum函数就会脱掉在sum内部的list comprehension外边一层括号,这样便可以保证输出的leaves都在同一维度内
# List of leaf labels for each branch
return sum([leaves(b) for b in branches(tree)],[])
def increment_leaves(t):
'''Return a tree like t but with leaf labels incremented.'''
if is_leaf(t):
return tree(label(t) + 1)
else:
# 注意这里必须用tree包裹递归函数,如果没有tree,那么最后返回的仅仅就是几个单独的leaf,无法构成完整的树
return tree(label(t),[increment_leaves(b) for b in branches(t)])
def increment(t):
'''Return a tree like t but with all labels incremented'''
# 递归结束条件为for循环终止,不需要单独设置base case
return tree(label(t) + 1, [increment_leaves(b) for b in branches(t)])
在有了一系列Tree Processing的函数之后,我们可以把树打印出来,并控制缩进,以更好的显示:
def print_tree(t,indent = 0):
print(' ' * indent + str(label(t)))
for b in branches(t):
print_tree(b, indent + 1)
在设计递归时,有两种方式:
- 使用return的方法控制递归进行
- 将需要跟踪的变量以函数参数的形式传入
对于第二种方法,如:
numbers = tree(3,[tree(4),tree(5,[tree(6)])]) # 分别统计从root到每一个叶结点的label总和 def print_nums(t,so_far): so_far = so_far + label(t) if is_leaf(t): print(so_far) else: for b in branches(t): print_sums(b,so_far)
在Tree的相关递归函数中我们可以发现,他的思路其实是和之前的递归类似的,从一个节点到分支的过程,其实就是在进行Recursion decomposition,同先前的递归一样,在书写函数时也只需要考虑下边一层的情况即可(即第(n-1)层可能存在的1、2、3、4…个节点如何处理)
lab 05
Define the function
add_trees, which takes in two trees and returns a new tree where each corresponding node from the first tree is added with the node from the second tree. If a node at any particular position is present in one tree but not the other, it should be present in the new tree as well.
首先思考下base case,可以将t1与t2为叶结点的情况合并在一起:
def add_trees(t1,t2):
if is_leaf(t1) or is_leaf(t2):
return tree(label(t1)+label(t2),branches(t1)+branches(t2))
else:
......
如果两者均不是叶结点,我们需要对两个树同时进行遍历(递归),这就需要用到拉链函数,同时最后的返回值一定是使用tree函数进行构造的,所以基本的框架应该是:
else:
return tree(label(t1)+label(t2),[add_trees(b[0],b[1]) for b in zip(branches(t1),branches(t2))])
显然,如果两树的构造完全相同,这么做是没有问题的,但是当树的构造不同时,直接使用zip函数会导致数据丢失,所以我们下边要解决的问题是将构造不同的两树变成相同的:
else:
branch_t1 = branches(t1)
branch_t2 = branches(t2)
t1_len = len(branch_t1)
t2_len = len(branch_t2)
if t1_len < t2_len:
branch_t1 += [tree(0) for _ in range(t2_len-t1_len)]
if t1_len > t2_len:
branch_t2 += [tree(0) for _ in range(t1_len - t2_len)]
技巧就是把原先不存在的节点用0节点填补上。
最后得到完整的递归函数:
def add_trees(t1,t2):
if is_leaf(t1) or is_leaf(t2):
return tree(label(t1) + label(t2),branches(t1) + branches(t2))
else:
branch_t1 = branches(t1)
branch_t2 = branches(t2)
t1_len = len(branch_t1)
t2_len = len(branch_t2)
if t1_len < t2_len:
branch_t1 += [tree(0) for _ in range(t2_len - t1_len)]
if t1_len > t2_len:
branch_t2 += [tree(0) for _ in range(t1_len - t2_len)]
return tree(label(t1)+label(t2),[add_trees(b[0],b[1]) for b in zip(branch_t1,branch_t2)])
disc 05
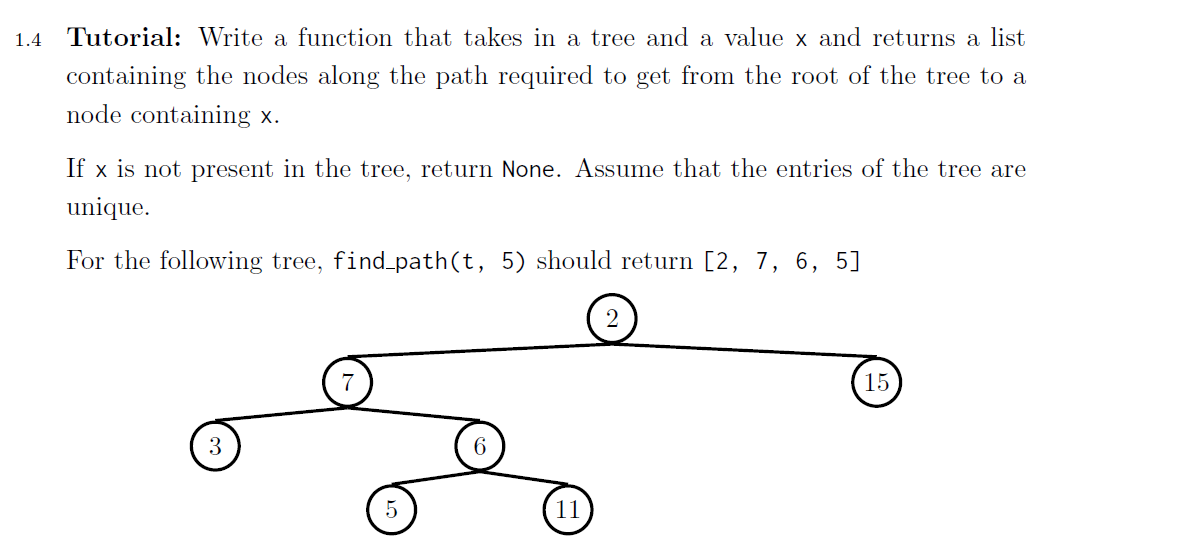
还是先来思考base case:
因为这道题最终并不是要构造一个树,所以base case不要理所应当的写作is_leaf,根据题目,在我们找到x时就应当返回带有x的列表,所以很容易想到:
def find_path(tree,x):
if label(tree) == x:
return [x]
接下来考虑是否可以用list comprehension的形式直接递归,但是我们想到list comprehension会将所有节点全部输出,但在遇到不存在x的路径时,根据题目要求需要返回None,所以为了更加清晰,我们将for循环拉出来写:
def find_path(tree,x):
if label(tree) == x:
return [x]
for b in branches(tree):
path = find_path(b,x)
# 如果已经找到了x所在的位置,则返回,否则继续for循环遍历分支
if path:
return [label(tree)] + path
仿照上边这道题:
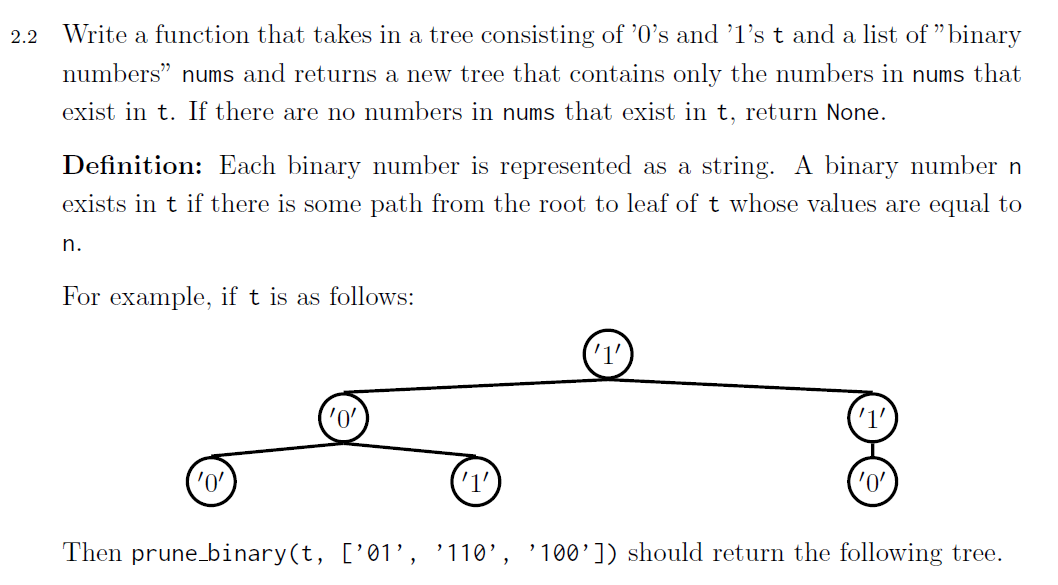
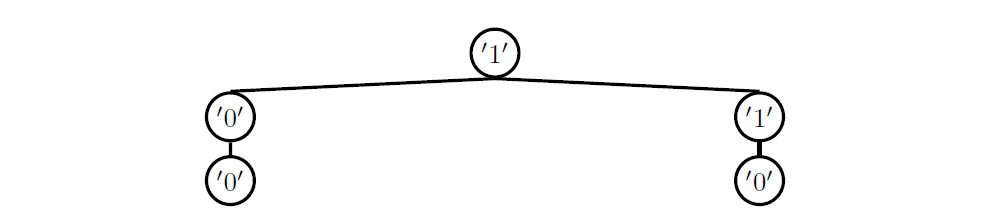
注意这道题最后是要返回一个tree的,但是和上一道题目相同,也是只包含了部分满足条件的节点,所以到这里,我们可以明白两件事:
- base case极大概率为
is_leaf() - 递归主体中的for循环不能使用
list comprehension的形式 - 函数最后要使用
tree函数return
def prune_binary(t,nums):
if is_leaf(t):
if label(t) in nums:
return t
return None
在递归主体中,我们需要完成两件事:
- 把列表中的元素的某几个字母抽出来,和分支节点比对,如果一样,就把对应元素中余下的字符传下去,如果不一样,就把那个元素直接扔掉吧
- 因为可能存在多个路径,我们最后要组合成一个完整的树
首先看第二点,其实list comprehension的另一种写法是:
next_branch = []
for b in branches(tree):
cur_f = f(x)
next_branch = next_branch + [cur_f]
return tree(label(tree),next_branch)
在这种写法中,next_branch的作用就是将某个节点下对应的所有branch组合起来,我们正是利用这一点来解决上边这道问题。
其次对于第一点,把伪代码实现出来:
next_valid_nums = [n[1:] for n in nums if label(t) == nums[0]]
至此,程序的大致结构已经确定了:
def prune_binary(t,nums):
if is_leaf(t):
if label(t) in nums:
return t
return None
else:
next_valid_nums = [n[1:] for n in nums if label(t) == nums[0]]
next_branch = []
for b in branches(tree):
pruned_branch = pruned_binary(b,next_valid_nums)
next_branch = next_branch + [pruned_branch]
#此处的return语句必须独立于for循环之外,否则一条分支结束了就回家了
return tree(label(tree),next_branch)
但同时注意到,在base case中存在返回None的可能性,如果pruned_binary一旦返回None,其实整个分支也就没有保留的必要了。所以我们需要加上一些判断语句,保证程序运行正确:
def prune_binary(t,nums):
if is_leaf(t):
if label(t) in nums:
return t
return None
else:
next_valid_nums = [n[1:] for n in nums if label(t) == nums[0]]
next_branch = []
for b in branches(tree):
pruned_branch = pruned_binary(b,next_valid_nums)
if pruned_branch is not None:
next_branch = next_branch + [pruned_branch]
if not new_branches:
return None
return tree(label(tree),next_branch)
F20 Lecture16 Q&A (Recursion->Tree+Higher Order Function)
1

def profit(t):
'''Return the max profit'''
return helper(t, False)
为什么需要一个helper函数?因为考虑到题目设置:对于某个节点
b,若它的父节点已被使用,则b不能被使用;如果父节点没有使用,那我们可以选择使用b或者不使用b,这也决定了接下来b的子节点能否被使用。这意味着需要跟踪一个额外的父节点是否已被使用的参数,所以需要建立一个helper函数。
def helper(t, used_parent):
# 如果已经使用了父节点,则下一个节点(该节点)不可使用,将flag设置为False就直接跳过这个if
if used_parent:
return sum([helper(b,False) for b in branches(t)])
else:
# 不使用父节点,分为用该节点/不用该节点两种情况,如果使用此节点,则下次递归(其子节点要跳过,即进入上边的if里)
use_current_total = label(t) + sum([helper(b,True) for b in branches(t)])
# 不使用此节点,则还需要考虑其子节点是否要使用,下次还要进入这里的else
skip_current_label= 0 + sum([helper(b,False) for b in branches(t)])
return max(use_current_total, skip_current_label)
2
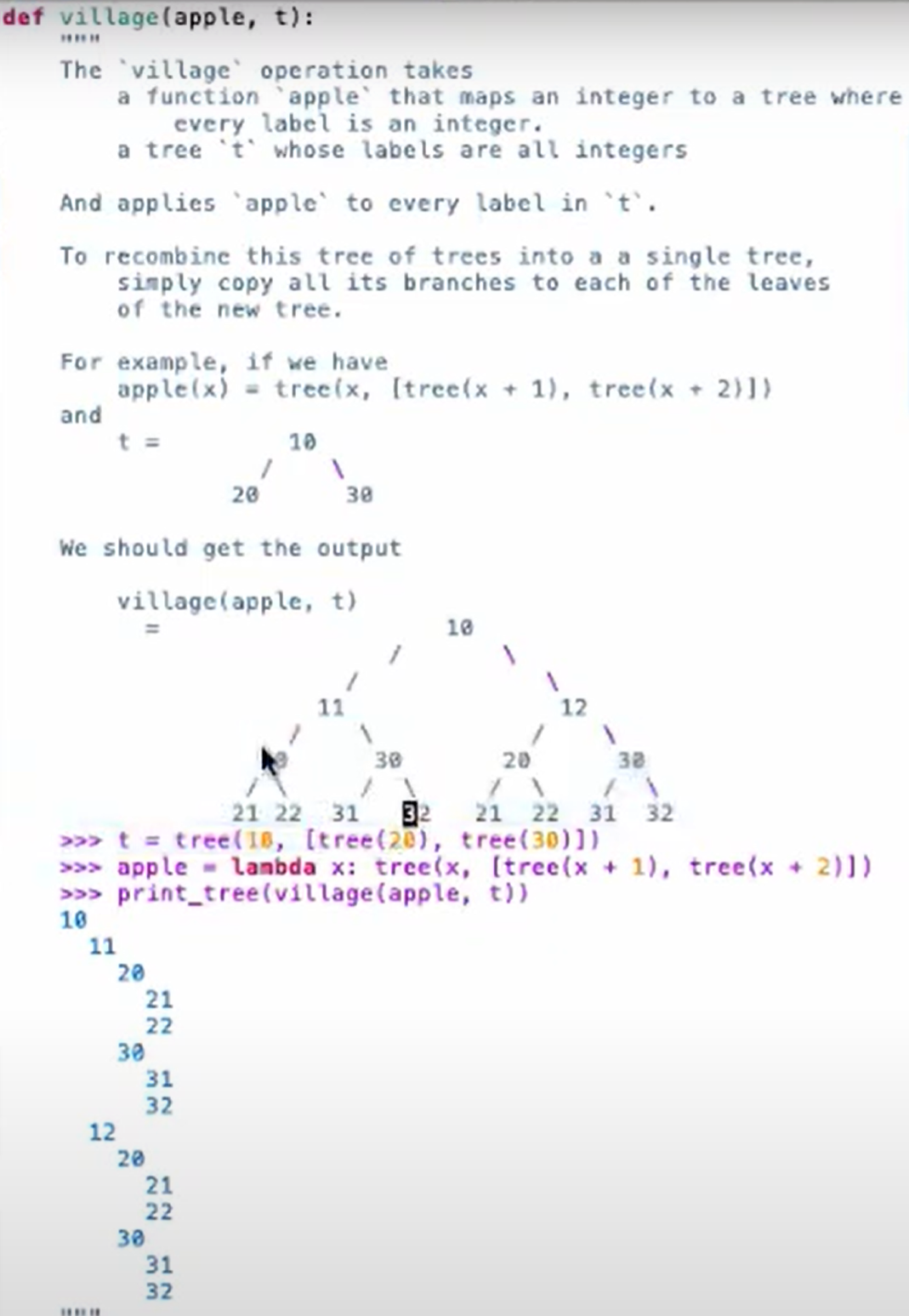
题目提供了一些基本的框架,这里不单独列出框架了,直接写(两种写法,我的做法和教授的不一样):
因为要同时跟踪已经加上的节点,将其作为原来的branches的root,同时还要跟踪未处理的branches,所以建立嵌套函数:
def village(apple, t):
'''Grafts the given branches 'bs' onto each leaf of the given tree 't', returning a new tree '''
def graft(t,bs):
if is_leaf(t):
return tree(label(t), bs)
new_branches = [graft(b,bs) for b in branches(t)]
return tree(label(t), new_branches)
base_t = apple(label(t))
bs = [village(apple,b) for b in branches(t)]
return graft(base_t,bs)
为什么要这么写?想法是通过变量base_t将节点扩展,利用bs遍历原树,之后通过graft(base_t,bs)函数传入扩展节点,并把添加节点的工作放在graft函数内部,与之前一样使用list comprehension的方法。也就是说大的目标有两个:
- 遍历原树,keep tracking of every nodes of the original tree
- 根据要求添加节点并构造新树
这道题也可以这么写:
def village(apple, t):
def graft(t, bs):
# 叶结点
if bs is None:
return t
new_branches = [tree(label(b), bs) for b in branches(base_t)]
return tree(label(t), [tree(label(b), [village(apple, branch) for branch in branches(b)]) for b in new_branches])
base_t = apple(label(t))
bs = branches(t)
return graft(base_t, bs)
这种方法的想法是把所有的递归工作放到内部函数中去,所以在叶结点的处理条件上有些改变,相对直观,内部函数的new_branch代表了经过apple处理后的所有分支。那么接下来要考察的就是除了root和刚才添加的apple生成节点了。
3 (Summer 2020 mt2 Q2)
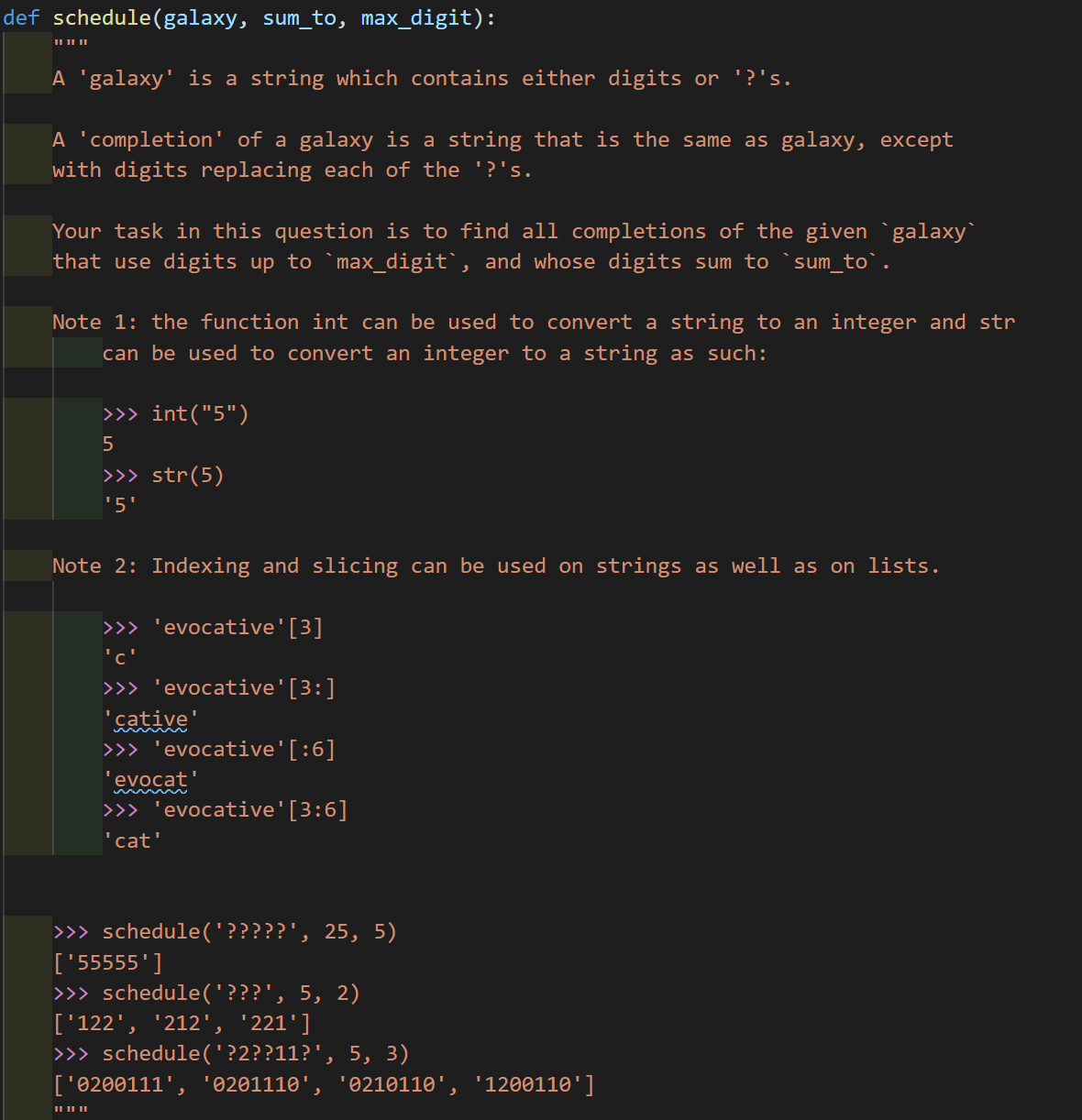
这道题目我尝试过使用一般的递归形式去做,但是发现会很麻烦…要返回的形式比较古怪,所以题目本身给出的模板里增加一个index标志跟踪字符位置是没有问题的,这会大大减少操作难度。
def schedule(galaxy, sum_to, max_digit):
def schedule_helper(galaxy, sum_sofar, index):
if index == len(galaxy) and sum_sofar == sum_to:
# 敏锐捕捉到,这个形式下返回的galaxy是完整的
return [galaxy]
elif sum_sofar > sum_to or (sum_sofar < sum_to and index == len(galaxy)):
return []
elif galaxy[index] != '?':
return schedule_helper(galaxy, sum_sofar + int(galaxy[index]), index + 1)
ans = []
for x in range(max_digit + 1):
# 关键的处理行
modified_galaxy = galaxy[0:index] + str(x) + galaxy[index + 1:]
ans = ans + schedule_helper(modified_galaxy, sum_sofar + x, index + 1)
return ans
return schedule_helper(galaxy, 0, 0)
卡住的点主要有三个:
- 敏锐捕捉到,base case中这个
[]返回值形式下的galaxy是完整的 index对准的是下一个即将处理的数字位置,而不是已经处理过的数字位置- 如果要保持
galaxy数组长度一致,如何去更改其中的某一位字符?
再考虑清楚这三点之后,余下的工作就比较清楚了:
- Base Case: 当遍历完最后一位数字,并且数字之和恰好为
sum_to时,把已经调整完毕的galaxy字符串以list的形式返回; - ERROR: 如果已经遍历完但是
sum还是不到设定值或者已经超过设定值的情况下,舍弃结果,返回空数组; - 如果指定位置的字符不为
'?',则保持galaxy不动; - 反之,在
max_digit的限制下对所有可能的数字递归选择,并使用切片操作更改指定位置的'?'为我们当前选定的数字x
因为源字符串中至少存在一个
'?',所以只需要在for循环内部对ans进行操作即可
这道题也可以用
yield做:def schedule(galaxy, sum_to, max_digit): def schedule_helper(galaxy, sum_sofar, index): if index == len(galaxy) and sum_sofar == sum_to: # 敏锐捕捉到,这个形式下返回的galaxy是完整的 # return [galaxy] yield galaxy elif sum_sofar > sum_to or (sum_sofar < sum_to and index == len(galaxy)): # return [] return elif galaxy[index] != '?': # return schedule_helper(galaxy, sum_sofar + int(galaxy[index]), index + 1) yield from schedule_helper(galaxy, sum_sofar + int(galaxy[index]), index + 1) # ans = [] for x in range(max_digit + 1): # 关键的处理行 modified_galaxy = galaxy[0:index] + str(x) + galaxy[index + 1:] # ans = ans + schedule_helper(modified_galaxy, sum_sofar + x, index + 1) yield from schedule_helper(modified_galaxy, sum_sofar + x, index + 1) # return ans (可以参考下边yield以list代写的简单例子) # return schedule_helper(galaxy, 0, 0) return list(schedule_helper(galaxy, 0, 0))
为什么上边结束递归时使用的是yield from而非yield?如果思考递归返回的流程可以发现,单独的yield会导致形成一个嵌套的generator;但是yield from可以保证每次都返回一层的生成器。
4
Print all the paths from the root of a tree to one of its leaves
>>> t = tree(1,[tree(2,[tree(3)]),tree(4)]) >>> print_all_paths(t) [1,2,3] [1,4]
之前我对这道题目的想法是:使用递归遍历节点,每当回到最外层循环时,就使用[]将已经遍历的节点包裹起来,但是这么做存在两个问题:
- 程序本身无法得知何时返回到最外层循环,我们也无法得知树的深度,所以无法使用
helper函数添加index遍历 - 按照一般的
tree的遍历方式,每次返回最外层循环时,已经是在root的分支里了,但是为了统计所有的路径,还需要把root加进去才行
所以教授的解法是,一上来先做一个程序抽象:
def print_all_paths(t):
'''Print all the paths from the root to a leaf'''
for path in all_paths(t):
print(path)
下边我们需要考虑all_paths这个函数如何实现。
首先按照tree的分支遍历方式:
def all_paths(t):
if is_leaf(t):
yield [label(t)]
for b in branches(t):
# What should be done next?
如果这里让我来写的话,估计会写成path = path + all_path(b)的形式,但仔细思考这种方法会导致各个独立的path无法分隔。所以为了在branches中也能将path分隔开,我们选择再加一层for循环来解决这个问题:
def all_paths(t):
if is_leaf(t):
yield [label(t)]
for b in branches(t):
for path in all_paths(b):
yield [label(t)] + path
需要注意的是,这种写法只适用于yield,因为yield会自动保存遍历信息,这给此类的遍历并保存所有已遍历信息的题目带来了很大便利,反之如果使用return,那么需要一个数组来全程跟进(贯穿)已经遍历过的节点,所以我们可以在函数参数中加一个数组res,用于跟踪遍历节点:
def all_paths2(res,t):
res.append(label(t))
if is_leaf(t):
return [res]
else:
ans = []
for b in branches(t):
ans += all_paths(res.copy(),b)
return ans
需要注意的是,在上边的程序中,res.copy()是必要的,因为python是传递引用,为了将同一层的节点遍历数组分隔开,必须使用copy()以免把所有的节点添加到同一个数组中。
F20 Lecture 15(List & Tuple Mutable)
List的Mutable性质 & Tuple的unmutable性质
- Mutable Default Arguments are Dangerous
函数的默认参数随函数本体一起创建,在使用过程中始终维护同一块内存空间

- List-addition & slicing
s = [2,3]
t = [5,6]
a = s + [t]
b = a[1:]
a[1] = 9
b[1][1] = 0
>>> s
[2,3]
>>> t
[5,0]
>>> a
[2,9,[5,0]]
>>> b
[3,[5,0]]
这里需要注意两个问题:
a = a + b # 不同于c.append(a)
这条+语句会为等式右侧的a与b分别创建一个全新的list,所以改变原始的a与b的值并不会影响相加生成后的列表a,这与append函数不同。
a += b # 不同于a = a + b
python中的+=号不完全等同于+,在这里,如果后续改变了b的值,则生成的a也会被改变。
s = [2,3] t = [5,6] a = s + [t]
[t]作为一个整体,可以理解为是[]经过append操作的产物,所以在这样的+操作中,创建的是[],之后指向原先的t数组所在的位置,所以此时改变t,则会改变生成的a的值。
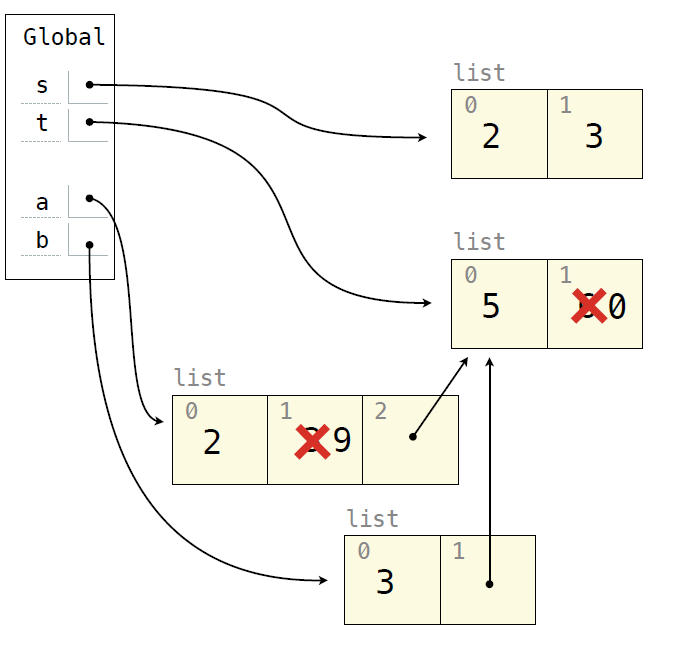
s[0:0] = t
意为在0处插入整个t序列(s[1:1]同理,不论插入序列的长度多少,因为使用的是slicing语法)
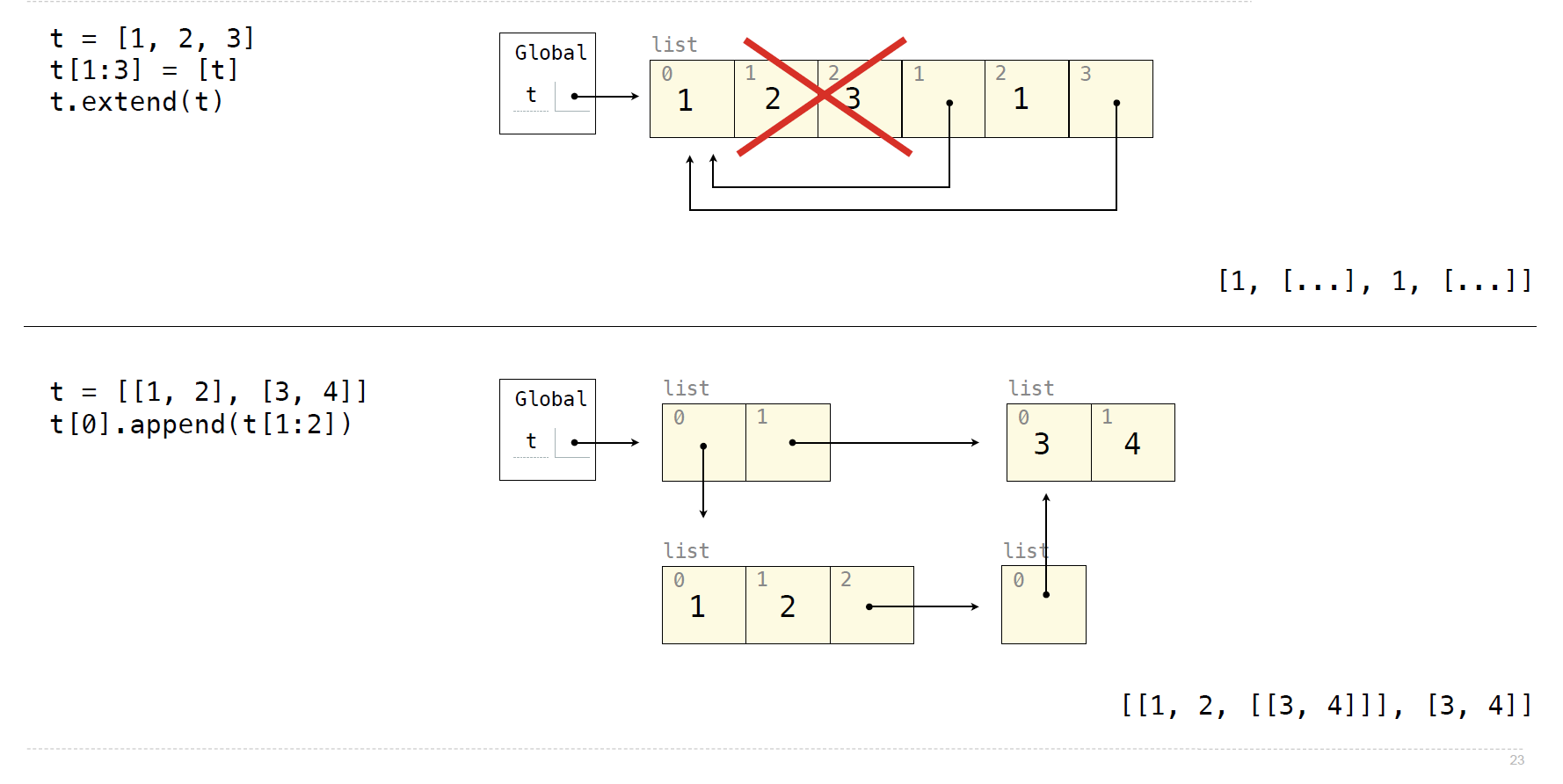
list()会创建一个新的对象- Lists in Lists in Lists in Environment Diagrams
- Tuple中的list数据可以被更改(因为指向的是单独开辟的另一块内存区域而不直接位于
tuple的内存块内)
F20 Lecture 16 - Nonlocal
Python Particulars
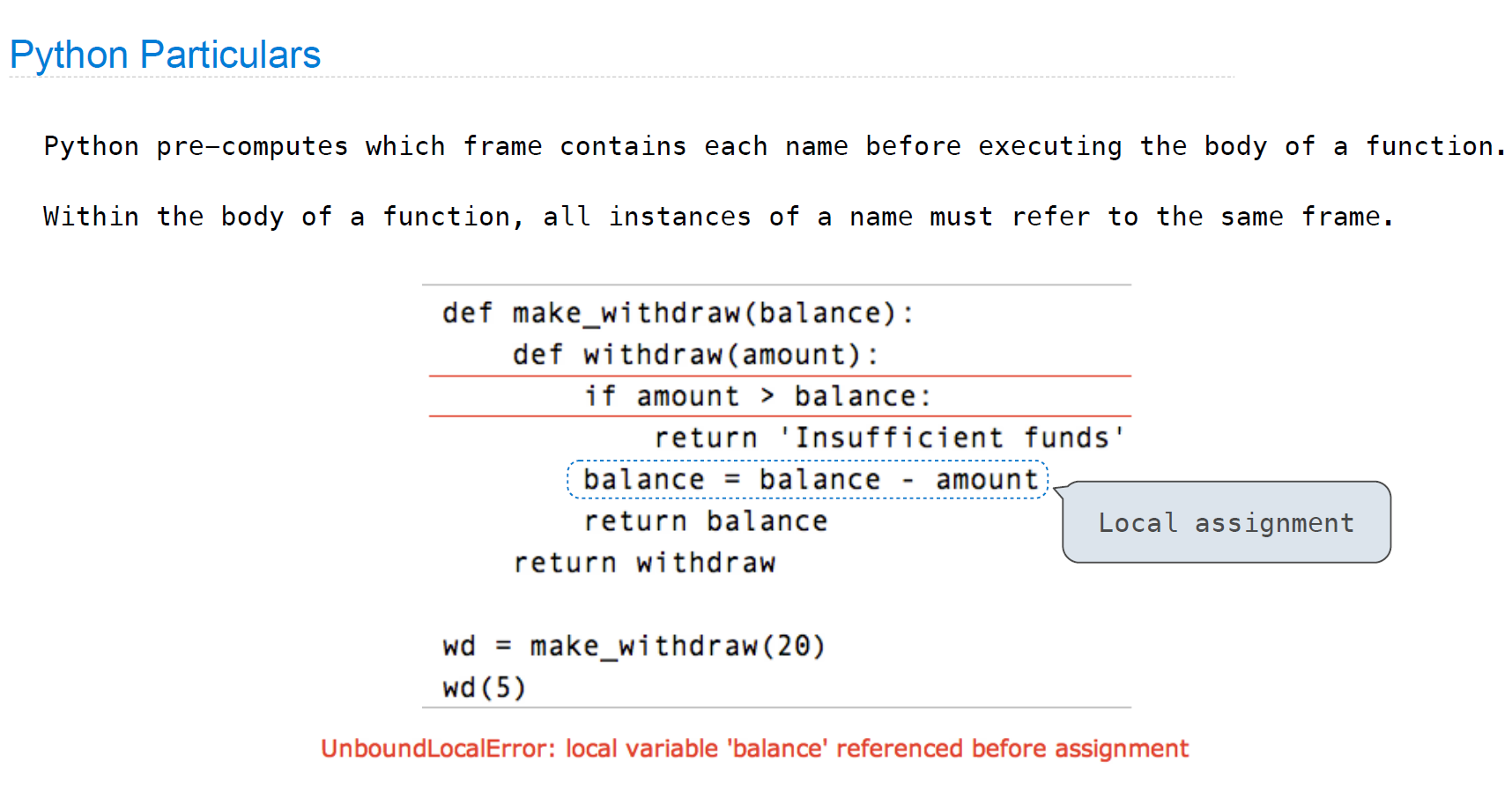
但是nonlocal关键字解决了这个问题:
def make_withdraw(balance):
def withdraw(amount):
nonlocal balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
wd = make_withdraw(20)
print(wd(5))
F20 Lecture 17 (Iterator & Generator)
Iterator
iter(iterable)-返回迭代器对象 next(iterator)-取出其中的值# Dictionary Iteration iter(dic.keys()) iter(dic.values()) iter(dic.items())Built-in Functions for Iteration

- 迭代器对象在被读取元素之后,即会将被读取的元素从迭代器对象中去除
s = [[1,2],3,4,5]
t = iter(s)
next(t)
next(t)
>>> list(t)
[4,5]
- 若字典已被开始读取,则中途不可以改变
size,但是可以改变未读取元素的值
d = {'one':1,'two':2}
k=iter(d)
next(k)
# 下边这句会报错,dictionary changed size during iteration
d['zero'] = 0
- for循环既可以遍历
list,也可以遍历迭代器,但是迭代器在遍历完毕之后不能再次使用了
To better understand the iterator, here is an example in the disc:

Generator
yield返回给调用者一个生成器对象
generator function is a function that yields values instead of returning them
A normal function returns once; a generator function can yield multiple times
A generator is an iterator created automatically by calling a generator function
When a generator function is called, it returns a generator that iterates over its yields
在遇到yield时,程序会暂停(保存局部变量),所以每次执行,都只会执行一个生成器对象:
def plus_minus(x):
yield x
yield -x
t = plus_minus(3)
>>> next(t)
3
>>> next(t)
-3
yield from从一个可迭代对象或者迭代器中yield所有值
Yield & Recursion
def prefixes(s):
if s:
yield from prefixes(s[:-1])
yield s
为了更加深刻的理解yield,我们可以展开分析一下上边这个简单的递归:
首先写成标准for循环的形式:
def prefixes(s):
if s:
for x in prefixes(s[:-1]):
yield x
yield s
每一次函数返回,都会把函数体中所有的generator对象传递回去,并且在上一级函数执行完毕之后,生成器对象又多了一个(yield s),逐次递增。
如果不使用yield,也可以实现这个功能:
def prefixes(s):
result = []
if s:
for x in prefixes(s[:-1]):
result.append(x)
result.append(s)
return result
这是一种常见的逐次减少(增多)顺序打印字符问题,在代码中未使用递归的单独语句可以被视为base case,其位置决定了我们打印字符的顺序,因为每一次递归都要去掉一个末尾的字符,而最终要得到所有的逐次输出结果,所以应该使用for循环的形式,递归prefixes(s[:-1])
A difficult Question(HW 04)
有了上边使用yield做递归的经验,来看这样一道题:
Q4: Generate Permutations
Given a sequence of unique elements, a permutation of the sequence is a list containing the elements of the sequence in some arbitrary order. For example,
[2, 1, 3],[1, 3, 2], and[3, 2, 1]are some of the permutations of the sequence[1, 2, 3].Implement
permutations, a generator function that takes in a sequenceseqand returns a generator that yields all permutations ofseq.Permutations may be yielded in any order. Note that the doctests test whether you are yielding all possible permutations, but not in any particular order. The built-in
sortedfunction takes in an iterable object and returns a list containing the elements of the iterable in non-decreasing order.Hint: If you had the permutations of all the elements in
seqnot including the first element, how could you use that to generate the permutations of the fullseq?Hint: If you’re having trouble getting started, see the hints video for this question for tips on how to approach this question.
这道题目的解题思路有很多,说两种解法:
解法1
先排permutations的第一个位置,有1,2,3三种方式,在排完第一位后,问题转化成为余下两个数字的permutations问题。与之前一样,因为我们要得到所有的可能性,比如在确定了第一位为1后,存在[1,2,3]与[1,3,2]两种情况,全部需要保存,故还是用一个for循环来进行递归处理,题目框架应为:
def permutations(seq):
# base case
if not seq:
yield []
else:
# 先选定第一个位置
for i in range(len(seq)):
start = seq[i]
# 也可以写成:rest = [seq[j] for j in range(len(s)) if i != j]
rest = seq[:i] + seq[i+1:]
for rest_permutation in premutations(rest):
yield [start] + rest_permutation
解法2
我们也可以用insert的思路来看待这道题目,比如先确定2,3的先后顺序,即先permutate (n-1)个,再将1插空:
def permutations(seq):
if not seq:
yield []
else:
first = seq[0]
rest = seq[1:]
for rest_permutation in permutations(rest):
# 选空插入
for i in range(len(seq)):
yield rest_permutation[:i] + [first] + rest_permutation[i:]
# 或者写作:
result = list(rest_permutation)
result.insert(i,first)
yield result
NOTICE
def filter_link(link, f):
if link is Link.empty:
yield Link.empty
# 不会如期执行if语句
if f(link.first):
yield link.first
filter_link(link.rest, f)
else:
filter_link(link.rest, f)
link = Link(1, Link(2, Link(3)))
g = filter_link(link, lambda x: x % 2 == 0)
next(g)
上边这个函数的执行结果并不会如预期,f(link.first)仅会在第一次运行时执行,之后的递归过程不会执行该函数,原因是因为函数整体中含有yield,它的运行不会和普通函数一样,每次filter_link的返回值都是一个generator object,除非我们迭代该生成器对象,否则其中的内容均不会执行,也就是说再进入下一个递归后,该函数根本不能正常执行,所以自然不会进入if判断语句了.
F20 Lecture 18 (Classes)
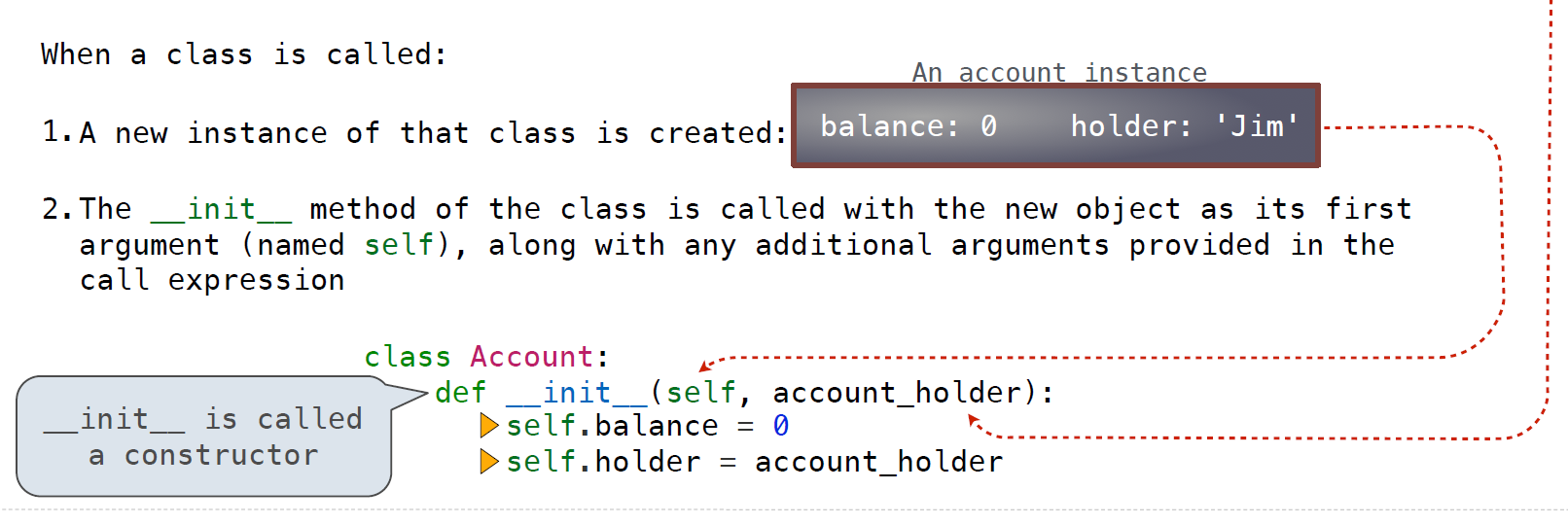
在设计类时几个需要注意的事项:
init method
Accessing Attributes

Bound methods
当进行实例调用时,隐式地将实例名称绑定到类方法的self参数上,比如现在有一个类Account,其中有一个method名为deposit,则我们可以通过两种方式调用该方法:
# as a function
Account.deposit(spock_account, 1001)
# as a bound method
spock_account.deposit(1000)
Evaluating a dot expression
.
- Evaluate the
to the left of the dot, which yields the object of the dot expression is matched against the instance attributes of that object; if an attribute with that name exists, its value is returned - If not,
is looked up in the class, which yields a class attribute value - That value is returned unless it is a function, in which case a bound method is returned instead
先在实例当中寻找对应的属性,如果没有,再到类实现中寻找
Class Attributes
class Account:
interest = 0.02
# A class attribute
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
# Additional methods would be defined here
>>> tom_account = Account('Tom')
>>> jim_account = Account('Jim')
>>> tom_account.interest
0.02
>>> jim_account.interest
0.02
但是考虑到
dot expression的实现过程(2 & 3),如果我们对示例中的class attribute进行更改,则此后直接更改class attribute不会对此实例中的该attribute造成任何影响:
kirk_account.interest = 0.08 >>> kirk_account.interest 0.08 >>> spock_account.interest 0.04 >>> Account.interest = 0.05 # changing the class attribute >>> spock_account.interest # changes instances without like-named instance attributes 0.05 >>> kirk_account.interest # but the existing instance attribute is unaffected 0.08
class也可以设立
@staticmethod方法,可以理解为C++类中的静态成员函数
F20 Lecture 19 (Classes-Attributes & Inheritance)
Assignments to Attributes
当我们对instance的attributes进行赋值操作时,首先会在本instance内寻找是否存在该attribute,如果不存在,则去找对应的class attribute,或者是在继承关系当中的父类的attribute,再把找到的attribute加入一开始的instance当中。反之如果instance中已经建立了该attribute,则直接对其进行更改。

Inheritance
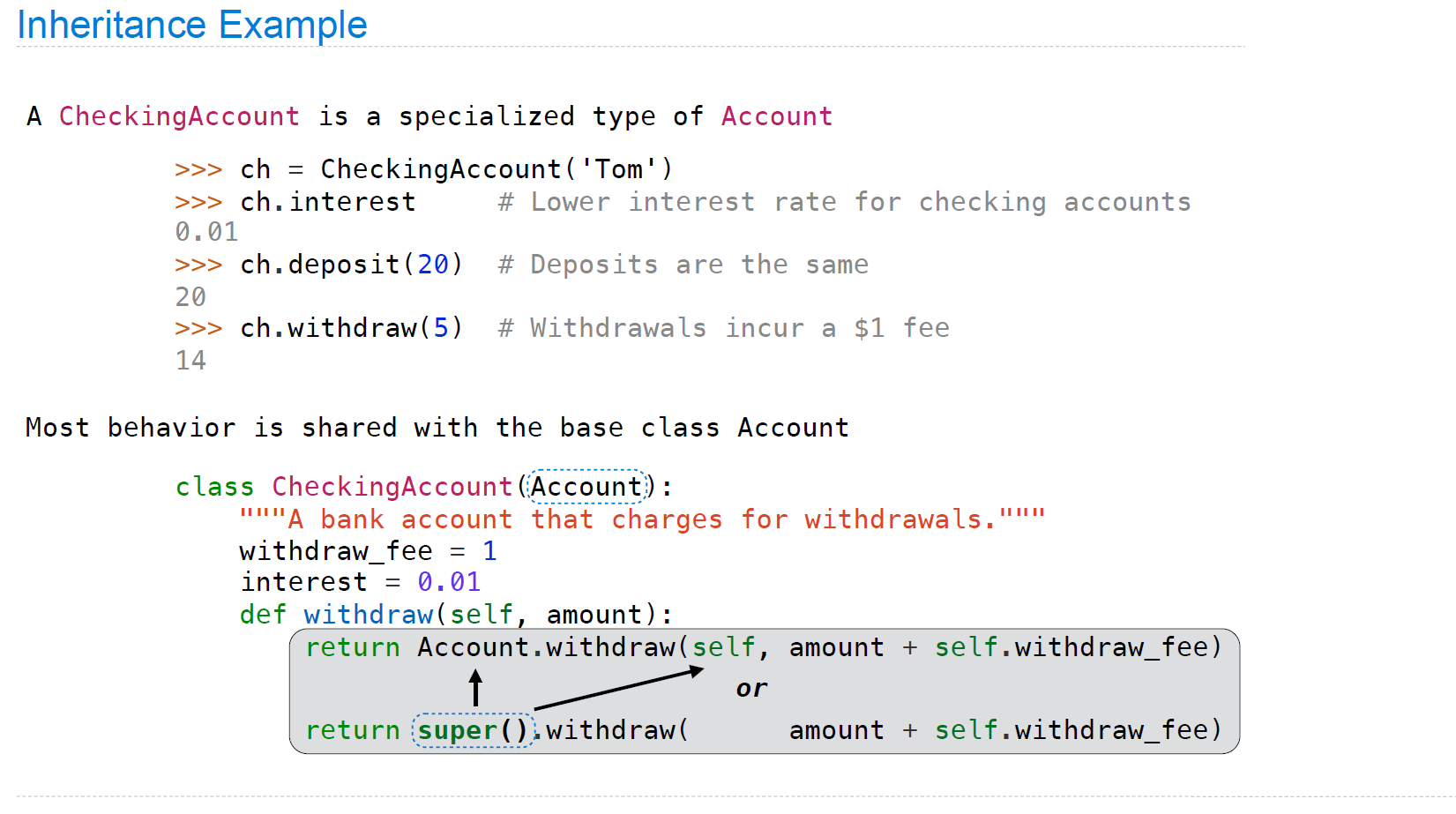
在设计继承时,要尽量做到Look up attributes on instances whenever possible,如果此例中使用的是withdraw而非self.withdraw,则假定有一批类实例,现在想更改其中某一个实例中的withdraw_fee,是不可实现的,因为我们只有更改类实现中的withdraw_fee值才可以对结果做出改变,而这将影响所有的类实例结果。
在继承关系中寻找attribute也是上个小节一样的道理,只是要注意基类的attributes不会自动复制到子类的实现中。也正因如此,对于一个子类实例,若调用了父类的某attribute,则程序会到父类中找到该attribute,并将其加入此子类实例中,与之前的从instance找class attribute是类似的流程。

Inheritance & Composition

class Bank:
def __init__(self):
self.accounts = []
def open_account(self, holder, amount, kind=Account):
account = kind(holder)
account.deposit(amount)
# Composition
self.account.append(account)
return account
def pay_interest(self):
for a in self.accounts:
a.deposit(a.balance * a.interest)
An Example
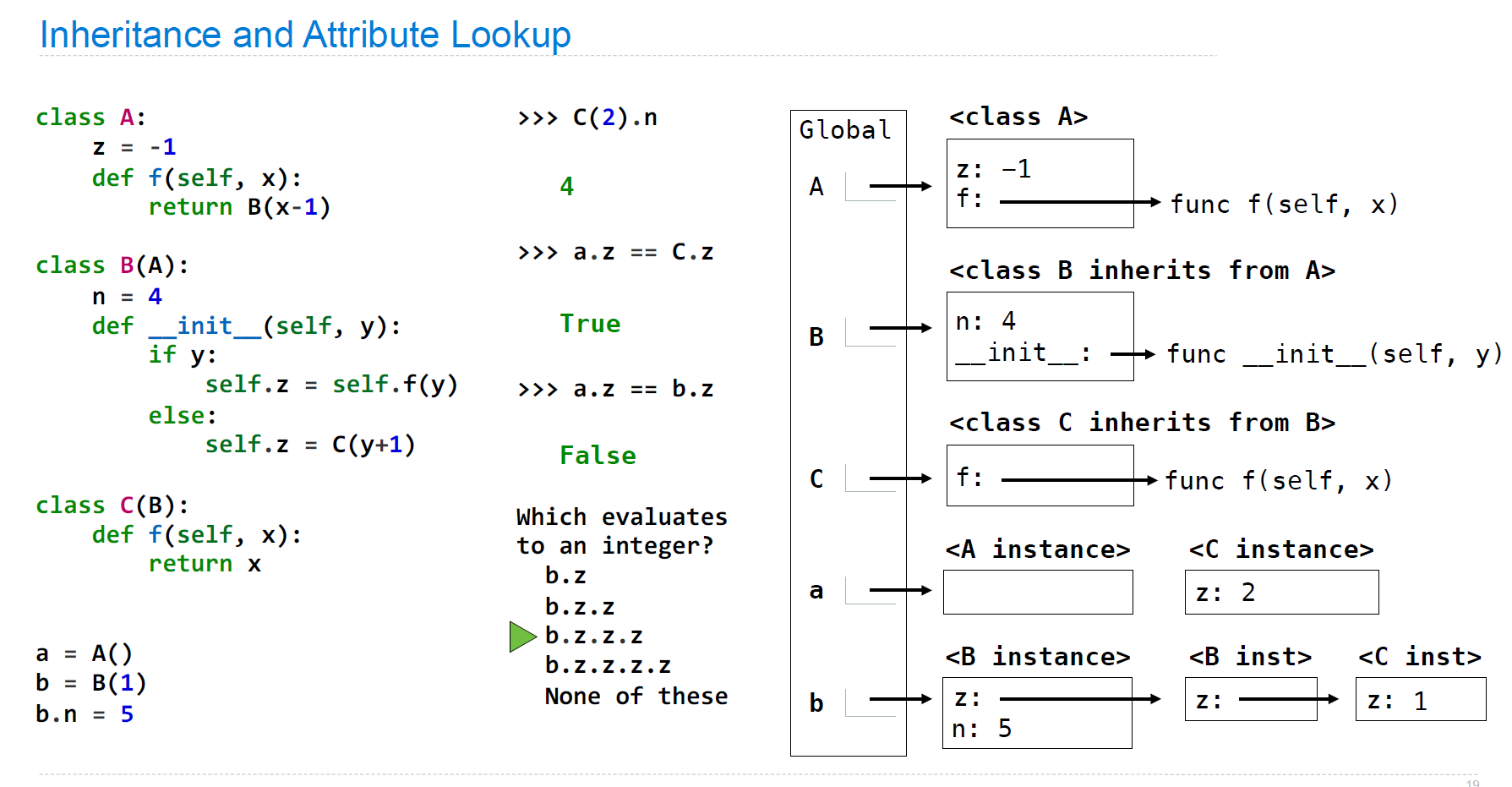
这里注意两个点:
- 在存在继承关系时,某一步中的
self究竟指代谁 C(2)是一个instance,找到父类B中的__init___,self此时指代C,并把父类B的z attribute加入利用C(2)创建的C instance中
Multiple Inheritance
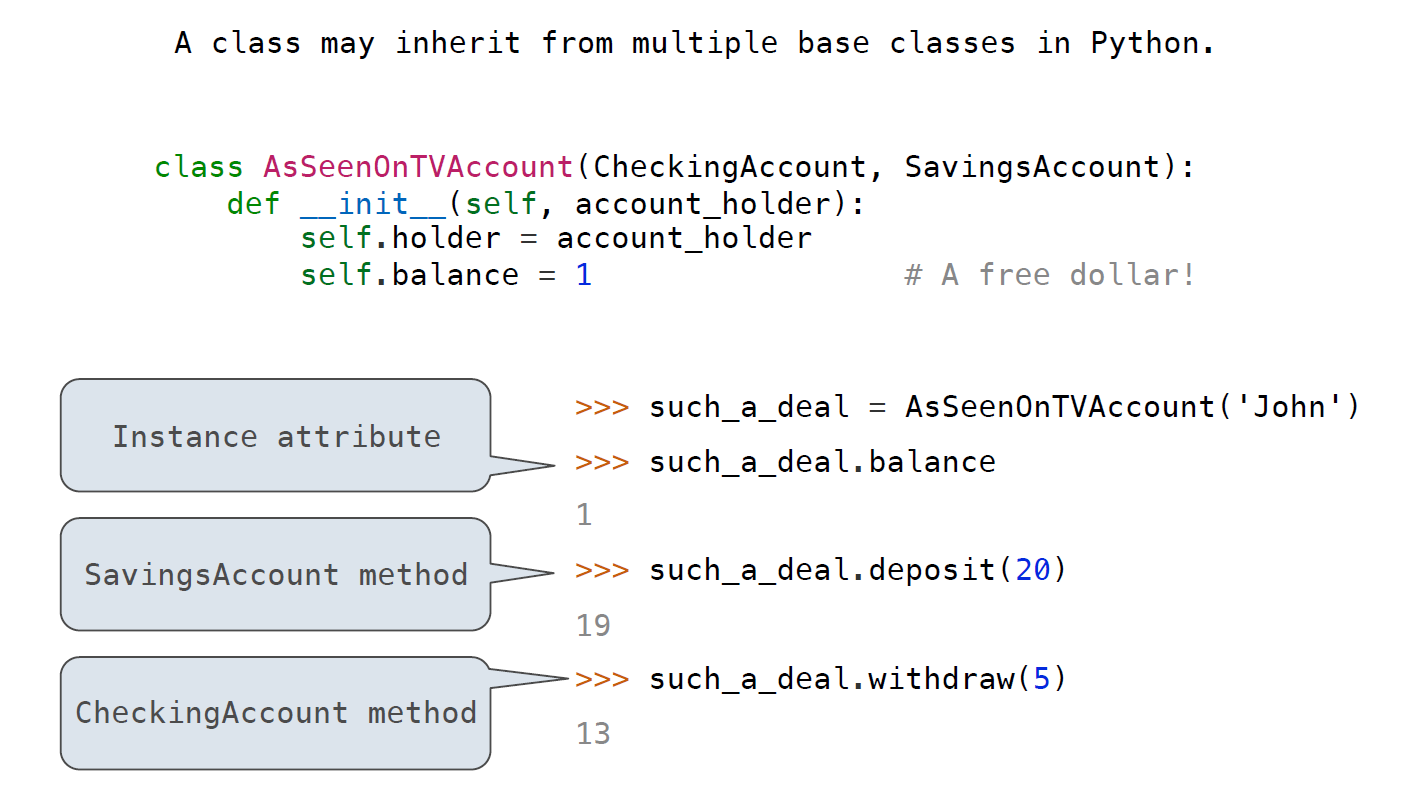
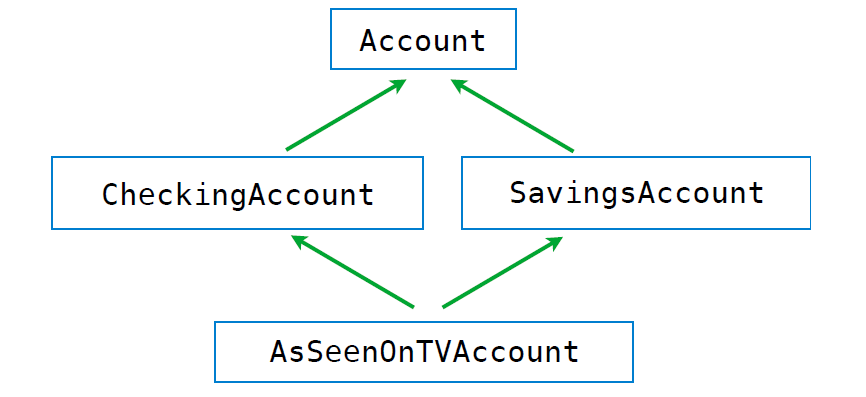
如果多个父类中存在相同的Attribute该怎么办?
In multiple inheritance, the attribute is first looked up in the current class. If it fails (which it does in this case since AsSeenOnTVAccount has no interest attribute), then the next place to search is in the parent class, and so on. If there are multiple parent classes (which there are in this case: CheckingAccount, SavingsAccount), then it returns the first one it finds by depth-first going from left to right between the parents.
可以用一个例子来说明该问题:
class Employee():
test1 =1
def __init__(self, id):
self.id = id # the employee id
class Student():
test1 = 2
def __init__(self, id, test):
self.test1 = test
self.id = id # the student id, different from employee id
class firm(Employee,Student):
test1 = 3
def __init__(self,Eid,Sid,test):
Employee.__init__(self,Eid)
Student.__init__(self,Sid,test)
result = firm(3,4,4)
print(result.test1)
print(result.id)
- 首先对于两个子类的同名的
instance attribute,获取到的表达式值取决于父类初始化的顺序,在firm类中,如果先初始化Employee,则result.id为Employee中的id值,反之为Student。 - 如果父类中的
class attribute与instance attribute同时存在,且同名,当我们试图获取子类中不存在但在父类中存在的attribute时,会首先考虑class attribute,因为子类建立时就已经接受了Student和Employee两个父类名参数,此后才调用了__init__方法。 - 如果多个父类中的同名的
class attribute,获取到的表达式的方法是从左向右搜索继承的父类名字,也即上边的英文解释所对应的方法。
F20 Lecture 20 (Representation)
String Representations
str
对应着print函数打印的方法,目的是方便人类阅读
repr
对应着interative python中打印的方法,目的是方便程序阅读
>>> from fractions import Fraction
>>> half = Fraction(1, 2)
>>> repr(half)
'Fraction(1, 2)'
>>> str(half)
'1/2'
Polymorphic Functions
str与repr通过在内部实现并调用__repr__和__str__方法,可以对多种数据类型操作(类似于C++中的操作符重载)
实现的规则如下:
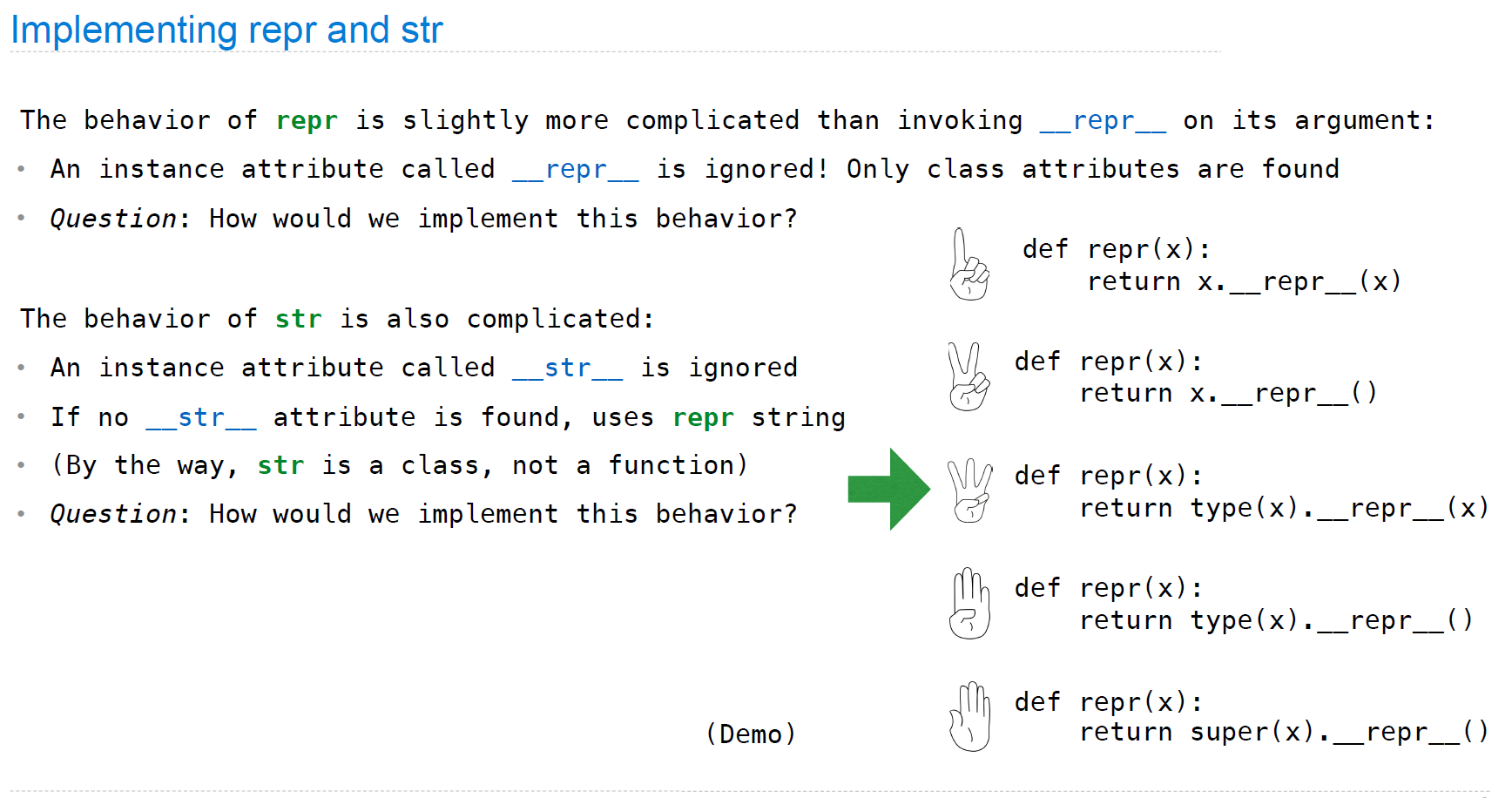
Interfaces

我们可以自己实现此类操作符重载(interface),这样在程序调用repr或者str时,就会使用我们的方法:
class Bear():
'''A Bear'''
def __init__(self):
self.__repr__ = lambda: 'oski'
self.__str__ = lambda: 'this bear'
def __repr(self):
return 'Bear()'
def __str(self):
return 'a bear'
>>> oski = Bear()
>>> print(oski)
>>> a bear
>>> print(str(oski))
>>> a bear
>>> print(repr(oski))
>>> Bear()
>>> print(oski.__str__)
>>> this bear
>>> print(oski.__repr__)
>>> oski
我们也可以自行实现str与repr方法:
def repr(x):
# 因为是class attribute
return type(x).__repr__(x)
def str(x):
t = type(x)
if hasattr(t, '__str__'):
return t.__str__(x)
else:
return repr(x)
Special Method Names in Python & Example
一个更综合的例子:
class Ratio:
def __init__(self,n,d):
self.numer = n
self.denom = d
def __repr__(self):
return 'Ratio({0},{1})'.format(self.numer,self.denom)
def __str__(self):
return '{0}/{1}'.format(self.numer,self.denom)
def __add__(self,other):
if isinstance(other, int):
n = self.numer + self.denom + other
d = self.denom
elif isinstance(other, Ratio):
n = self.numer * other.denom + self.denom * other.numer
d = self.denom * other.denom
elif isinstance(other, float):
return float(self) + other
g = gcd(n,d)
return Ratio(n//g, d//g)
# 令内置方法等价
__radd__ = __add__
def __float__(self):
return self.numer / self.denom
# 辗转相除法求最大公约数
def gcd(n, d):
while n != d:
n, d = min(n, d), abs(n-d)
return n
F20 Lecture 21 (Linked Lists & Trees)
isinstance:Return whether an object is an instance of a class or of a subclass thereof.
Linked Lists Implementation (Recursion)
class Link:
"""A linked list."""
empty = ()
def __init__(self, first, rest=empty):
assert rest is Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __repr__(self):
if self.rest:
rest_repr = ', ' + repr(self.rest)
else:
rest_repr = ''
return 'Link(' + repr(self.first) + rest_repr + ')'
def __str__(self):
string = '<'
while self.rest is not Link.empty:
string += str(self.first) + ' '
self = self.rest
return string + str(self.first) + '>'
square, odd = lambda x: x * x, lambda x: x % 2 == 1
list(map(square, filter(odd, range(1, 6)))) # [1, 9, 25]
def range_link(start, end):
"""Return a Link containing consecutive integers from start to end."""
if start >= end:
return Link.empty
else:
return Link(start, range_link(start + 1, end))
def map_link(f, s):
"""Return a Link that contains f(x) for each x in Link s."""
if s is Link.empty:
return s
else:
return Link(f(s.first), map_link(f, s.rest))
def filter_link(f, s):
"""Return a Link that contains only the elements x of Link s for which f(x)
is a true value."""
if s is Link.empty:
return s
filtered_rest = filter_link(f, s.rest)
if f(s.first):
return Link(s.first, filtered_rest)
else:
return filtered_rest
map_link(square, filter_link(odd, range_link(1, 6))) # Link(1, Link(9, Link(25)))
"""test1"""
>>> s = Link(3, Link(4, Link(5)))
>>> s
Link(3, Link(4, Link(5)))
>>> print(s)
<3 4 5>
>>> s.first
3
>>> s.rest
Link(4, Link(5))
>>> s.rest.first
4
>>> s.rest.first = 7
>>> s
Link(3, Link(7, Link(5)))
>>> s.first = 6
>>> s.rest.rest = Link.empty
>>> s
Link(6, Link(7))
>>> print(s)
<6 7>
>>> print(s.rest)
<7>
>>> t = Link(1, Link(Link(2, Link(3)), Link(4)))
>>> t
Link(1, Link(Link(2, Link(3)), Link(4)))
>>> print(t)
<1 <2 3> 4>
"""test2"""
>>> range_link(3, 6)
Link(3, Link(4, Link(5)))
"""test3"""
>>> map_link(square, range_link(3, 6))
Link(9, Link(16, Link(25)))
"""test4"""
>>> filter_link(odd, range_link(3, 6))
Link(3, Link(5))
__repr__函数还有另一种实现方法:
def __repr__(self):
# base case:
if not self.rest:
return 'Link(' + repr(self.first) + ')'
else:
return 'Link(' + repr(self.first) + ', ' + repr(self.rest) + ')'
这种思路是直接从base case开始写的,并在确定了recursive case的基本形式后对base case进行调整,而老师给出的做法是先写大框架,其中的rest_repr作为变量进行递归。
__str__函数的思路:
在一般情况下,从开头至末尾都是不需要有</>符号的,所以可以使用while循环
Tree Class Implementation (Recursion)
class Tree:
"""A tree is a label and a list of branches."""
def __init__(self, label, branches=[]):
self.label = label
for branch in branches:
assert isinstance(branch, Tree)
self.branches = list(branches)
def __repr__(self):
if self.branches:
branch_str = ', ' + repr(self.branches)
else:
branch_str = ''
return 'Tree({0}{1})'.format(repr(self.label), branch_str)
def __str__(self):
return '\n'.join(self.indented())
def indented(self):
lines = []
for b in self.branches:
# 每一个分支都会有好几行(包含好几层节点)
for line in b.indented():
# 保证同一层节点拥有同样的缩进,加一层则多一个缩进
lines.append(' ' + line)
return [str(self.label)] + lines
def is_leaf(self):
return not self.branches
def fib_tree(n):
"""A Fibonacci tree."""
if n == 0 or n == 1:
return Tree(n)
else:
left = fib_tree(n-2)
right = fib_tree(n-1)
fib_n = left.label + right.label
return Tree(fib_n, [left, right])
def leaves(tree):
"""Return the leaf values of a tree."""
if tree.is_leaf():
return [tree.label]
else:
return sum([leaves(b) for b in tree.branches], [])
def height(tree):
"""The height of a tree."""
if tree.is_leaf():
return 0
else:
return 1 + max([height(b) for b in tree.branches])
def prune(t, n):
"""Prune sub-trees whose label value is n."""
# 先裁剪再遍历
t.branches = [b for b in t.branches if b.label != n]
for b in t.branches:
prune(b, n)
"""test1"""
>>> print(fib_tree(4))
3
1
0
1
2
1
1
0
1
"""test2"""
>>> leaves(fib_tree(4))
[0, 1, 1, 0, 1]
"""test3"""
>>> t = fib_tree(5)
>>> prune(t, 1)
>>> print(t)
5
2
3
2
Ants – Optional Problem 4 (Status & Abstraction Barrier)
这道题可以总结两个值得注意的点:
- 程序抽象和
abstraction barrier
程序需要我们在四个位置进行修改,分别是make_slow,make_scare,apply_status和bee中的action成员函数。做好程序抽象的表现,或者说维持abstraction barrier的表现就是我们在make_slow和make_scare中虽然也要出现action的行为,但不会把action里的内容在这两个函数里复制粘贴一遍,我们要做的一定是调用action函数,但辅之以一定的限定条件。
换句话说,牵扯到状态改变的操作应当在make_slow与make_scare中完成,原本的action中只负责完成对应状态应当完成的事情。
def make_slow(action, bee):
"""Return a new action method that calls ACTION every other turn."""
# BEGIN Problem Optional 4
def do_change(gamestate):
if gamestate.time % 2 == 0:
action(gamestate)
return do_change
def make_scare(action, bee):
"""Return a new action method that makes the bee go backwards."""
# BEGIN Problem Optional 4
def do_change(gamestate):
bee.backwards = True
# 这里的action未必是一开始的action
action(gamestate)
bee.backwards = False
return do_change
比如,一个典型的例子就是这里的bee.backwards的设置,有很多网上的答案写的是有问题的,他们将bee.backwards=False这一步放到了bee.action的实现里,破坏了abstraction barrier。这样的设计会在如下的情况出现问题:
如果执行顺序是
make_scary->make_slow,自gamestate.time=0起始,在gamestate.time=1时,slow不做动作,也就是说没有进入bee.action方法里,则此时当gamestate.time=1的所有动作完毕后,bee.backwards仍保持True的状态,可是下次当gamestate.time=2时,make_scary动作结束,此时本应当返回前行,即bee.backwards=False,可是此时的bee.backwards仍维持了True的状态,会造成错误
- 状态机
这里是一个很好的状态机的实现案例,因为会遇到状态叠加的情况,而每一次增加status,都会调用apply_status函数。此后,动作bee.action会调用存储的不同的status,从最外层的status开始。所以我们要用bee.action将不同的状态按照先后顺序连接成完整的状态机。所以我们考虑使用如下方法:每次调用apply_status,即向状态机中增加状态时,先将当前的状态,即bee.action存储起来,接着把增加的状态(status)赋给bee.action。那么当下次再向状态机中增加status时,此时当前状态bee.action对应的是上一个被加入状态机的status,以此类推。
满足题意的设计如下:
def apply_status(status, bee, length):
"""Apply a status to a BEE that lasts for LENGTH turns."""
# BEGIN Problem Optional 4
previous_behavior = bee.action
do_change = status(bee.action, bee)
def action(gamestate):
nonlocal length
if length > 0:
do_change(gamestate)
length -= 1
else:
previous_behavior(gamestate)
bee.action = action
最后,在bee.action方法中,我们只需要实现make_scary对应状态即可:
if self.backwards:
destination = self.place.entrance
if isinstance(destination, Hive):
destination = self.place
HW05 (Linked Lists & Trees OOP)
迭代构建Linked Lists
通过迭代的方法遍历(构建)链表,是从列表末尾开始前往列表头部的,如果使用递归则是反过来:
(在不使用字符串相关操作的情况下)
def store_digits(n):
"""Stores the digits of a positive number n in a linked list."""
result = Link.empty
while n > 0:
result = Link(n % 10, result)
n //= 10
return result
L/R Fold Function of Linked Lists
函数构造相对简单,这里不再赘述,但是在某些题目中会用到:
- LFOLD:
>>> lst = Link(3, Link(2, Link(1)))
>>> foldl(lst, sub, 0) # (((0 - 3) - 2) - 1)
-6
>>> foldl(lst, add, 0) # (((0 + 3) + 2) + 1)
6
>>> foldl(lst, mul, 1) # (((1 * 3) * 2) * 1)
6
def foldl(link, fn, z):
if link is Link.empty:
return z
return foldl(link.rest, fn, fn(z, link.first))
- RFOLD:
def foldr(link, fn, z):
if link is Link.empty:
return z
return fn(link.first, foldr(link.rest, fn, z))
Filter with Fold
使用fold函数完成filter功能,其实主要难点在于对fn函数的设计,我们需要从一种抽象的角度来思考如何设计该函数:我们观察foldr的返回结构,fn接受两个参数,第一个是当前链表的头部节点值,第二个是即将要处理的rest序列,那么filter的fn就应该定义为:如果满足pred,则保留link.first,并继续递归rest部分;否则舍弃link.first,直接递归rest。
或者说得直接一点:fn在这里的功能就应该是,判定某个元素是否应当被滤除.
def filterl(lst, pred):
""" Filters LST based on PRED """
def filtered(x, y):
# 如果满足要求,则保留
if pred(x):
return Link(x, y)
return y
return foldr(lst, filtered, Link.empty)
链表翻转
这道题有两种解法,第一种是利用foldl函数,还是从抽象角度入手:
def reverse(lst):
""" Reverses LST with foldl """
return foldl(lst, lambda x, y: Link(y, x), Link.empty)
在这里,
x会是一个link list,y是要反转的值
亦或者,还有一种更经典的递归算法,可以参见这里:
def reverse2(lst):
if lst is Link.empty:
return lst
elif lst.rest is not Link.empty:
second, last = lst.rest, lst
lst = reverse2(second)
second.rest, last.rest = last, Link.empty
return lst
判定Valid BST
标准二叉树要满足以下条件:

注意,标准二叉树要求对某节点左侧子树和右侧子树的最大值和最小值位置有要求,而不是仅仅考察直接连接的左右节点。
这道题可以有两种解法,首先我们可以假定树符合要求,则我们可以通过如下函数分别获取最大值与最小值:
def bst_min(t):
"""Returns the min of t, if t has the structure of a valid BST."""
if t.is_leaf():
return t.label
return min(t.label, bst_min(t.branches[0]))
def bst_max(t):
"""Returns the max of t, if t has the structure of a valid BST."""
if t.is_leaf():
return t.label
return max(t.label, bst_max(t.branches[-1]))
此后分情况递归讨论即可。
另一种做法是,不先做树为Valid BST的假设,直接计算子树的最值,我们可以通过遍历出所有子树节点实现。方法可以直接看preorder那道题。
前序遍历Tree方法
首先,可以借鉴Tree类中的打印函数实现方法:
def indented(self):
lines = []
for b in self.branches:
# 每一个分支都会有好几行(包含好几层节点)
for line in b.indented():
# 保证同一层节点拥有同样的缩进,加一层则多一个缩进
lines.append(' ' + line)
return [str(self.label)] + lines
根据注释中的思路理解这种递归,同时按照递归问题的一般思路,这里也只考虑第一层遍历的节点,也就是
root的我下一层节点:假设在内层for循环中b.indented可以返回正确的值(其实这一步用了数学归纳法)那么内层的for循环会把所有的节点前边加上一个缩进,存储到lines里,之后循环下一个也在第一层的节点及其子树,最后把root加在最前边,说明算法成立!
类似地,写出前序遍历二叉树的函数:
def preorder(t):
label_lst = []
for b in t.branches:
# 假设bst可以正确返回第一层以下某个分支的所有节点,则经过推导,结果正确
for b1 in bst(b):
label_lst.append(b1)
return [t.label] + label_lst
或者写作:
def preorder(t):
if t.branches == []:
return [t.label]
flattened_children = []
for child in t.branches:
# 假设preorder在这里可以返回第一层以下某分支所有节点
flattened_children += preorder(child)
return [t.label] + flattened_children
也可以利用python的内置函数实现,不详细讨论:
def preorder_alt(t): return reduce(add, [preorder(child) for child in t.branches], [t.label])
完全二叉树 已知叶结点,求树结构数量
我们将一棵完全二叉树分为左半树和右半树,那么在n个叶结点中,所有的情况里左半树可以有1-(n-1)个节点:
def num_trees(n):
if n == 1:
return 1
for num_of_left_trees in range(1, n):
num_of_right_trees = n - num_of_left_trees
# 根据递归原则:
num_left_trees = num_trees(num_of_left_trees)
num_right_trees = num_trees(num_of_right_trees)
# 总数是相乘
return num_left_trees * num_right_trees
如果我们用一行代码解决这个问题:
def num_trees(n):
if n == 1:
return 1
return sum(num_trees(k) * num_trees(n-k) for k in range(1,n))
树的裁剪 (lab 09)
先裁剪,再遍历
def prune_small(t, n):
"""Prune the tree mutatively, keeping only the n branches
of each node with the smallest label."""
while len(t.branches) > n:
# 注意这里key必须是一个函数
largest = max(t.branches, key=lambda x: x.label)
t.branches.remove(largest)
for b in t.branches:
prune_small(b, n)
树的横向递归/遍历
disc 14

与普通的深度搜索方法不同,这道题使用的是广度搜索,所以自然而然的,我们尝试使用while循环,题目给出的template也是这样写的。思考while循环的功能:遍历同一层的所有分支,并把这些分支的label按照一层一个list的形式储存起来,最终选择数量最多的那一个。
于是我们想,需要一个数组levels储存节点label。在这之后,要想的问题是,遍历完一层之后,如何把下一层的所有节点(子树)存储起来,再遍历?
所以,我们想再借助一个数组,用来储存每次我们要遍历的下一层所有子树,直到空为止,while循环结束。
def widest_level(t):
levels = []
x = [t]
while x:
levels.append([t.label for x in x])
x = sum([t.branches for t in x],[])
return max(levels, key=len)
这里
sum的作用是把原本在不同的list里的很多个branches放到同一层的大list底下
Smalls & Bigs
bigs
Implement bigs, which takes a Tree instance t containing integer labels. It returns the number of nodes in t whose labels are larger than all labels of their ancestor nodes.
这道题的切入点应当是,需要track a list of ancestors,得到max(ancestors),如果满足node.label > max(ancestors),则符合要求。所以我们考虑使用Higher Order Function,用一个参数保存当前最大的节点值,之后分两种情况讨论,利用数学归纳法假定bigs(b, a.label)会返回正确的值,从而需要sum()处理统计结果:
def bigs(t):
def f(a, x):
if a.label > x:
return 1 + sum([bigs(b, a.label) for b in t.branches])
else:
return sum([bigs(b, x) for b in t.branches])
return f(t, t.label - 1)
这道题也可以使用Recursion Accumulation的方法去做,也即使用一个变量来保存节点数量,x代表the largest ancestor:
def bigs(t):
n = 0
def f(a, x):
nonlocal n
if a.label > x:
n += 1
for b in t.branches:
f(b, max(a.label, x))
f(t, t.label - 1)
return n
smalls
Implement smalls, which takes a Tree instance t containing integer labels. It returns the non-leaf nodes in t whose labels are smaller than any labels of their descendant nodes.
与bigs所不同的是,这里的要求针对的(或者说考察对象)是所有的子节点。
对于某个子树t,我们想要完成如下两个功能:
- Find smallest label in t
- Maybe add t to result
由于遍历过程是自顶向下的,所以我们的过程一定是,先遍历到叶结点,之后存储返回的满足要求的节点(设立一个数组result),同时完成比较大小的工作(一般在返回值处使用min)。
def smalls(t):
result = []
def process(t):
if t.is_leaf():
return t.label
else:
# find the smallest
smallest = min([process(b) for b in t.branches])
if t.label < smallest:
# add t to the result
result.append(t)
return min(smallest, t.label)
process(t)
return result
F20 Lecture 22 (Efficiency)
递归优化
def fib(n):
if n == 0 or n == 1:
return n
else:
return fib(n-2) + fib(n-1)
# Time
def count(f):
"""Return a counted version of f with a call_count attribute."""
def counted(*args):
counted.call_count += 1
return f(*args)
counted.call_count = 0
return counted
# Memoization
def memo(f):
"""Memoize f."""
cache = {}
def memoized(n):
if n not in cache:
cache[n] = f(n)
return cache[n]
return memoized
在python中,函数可以设置属性如
function.attribute,且不需要nonlocal等字眼
通过设置memo函数,我们可以大大提升运行速度,将已经计算过的值储存起来。在调用时,技巧是令fib=count(fib)以及fib=memo(fib),如此一来,通过变量fib调用的对象就会变成另外一个函数:
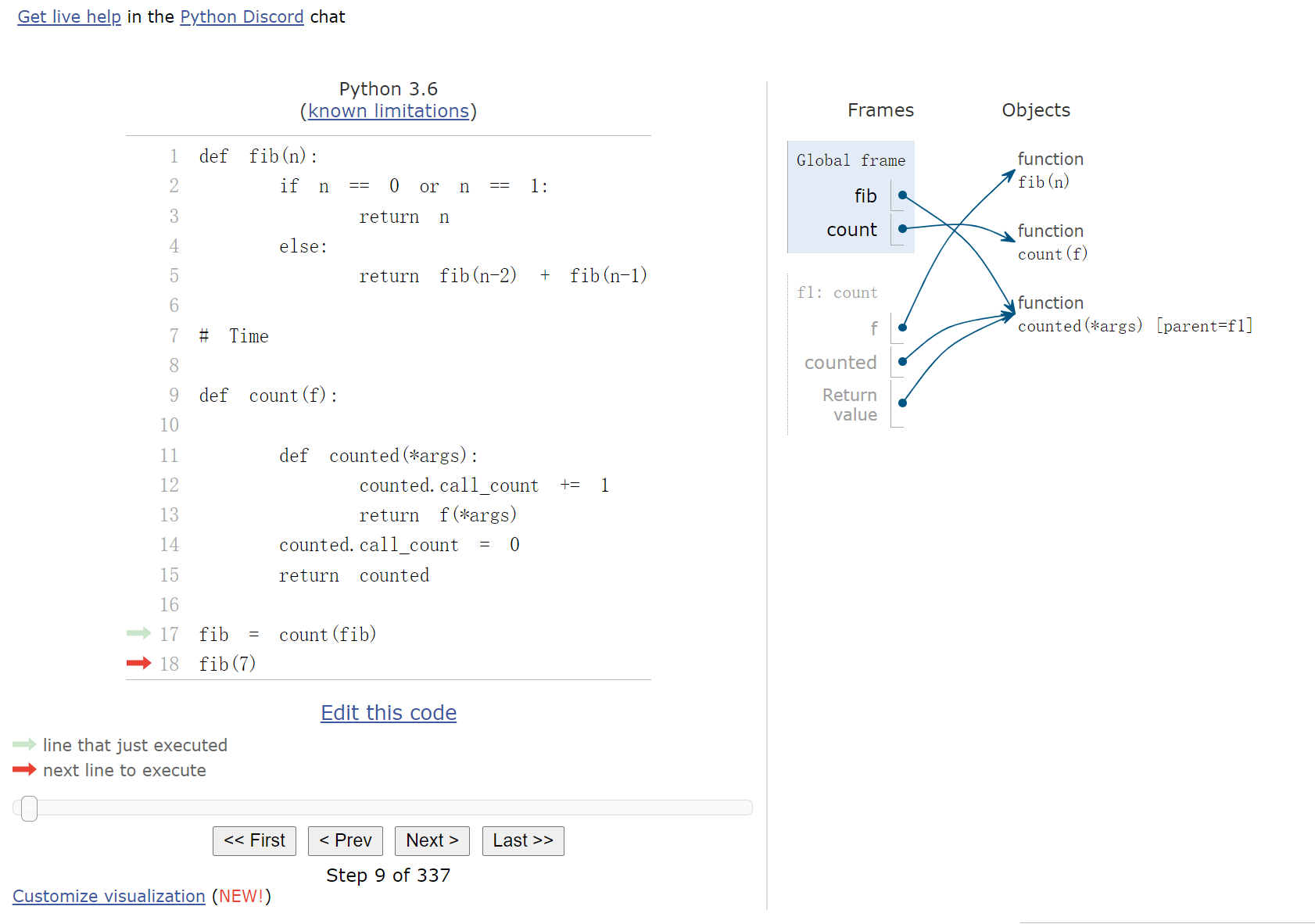
在fib=count(fib)中,等式右侧的参数fib先被绑定到函数count的参数f上,接下来等式左侧,原本是全局函数名的fib绑定到了count函数的返回值,也即counted(*args)上,此后,我们执行fib(x)执行的都是counted函数,而在进入counted内部后,f(*args)则会执行原本的fib函数。
fib = count(fib)
counted_fib = fib
fib = memo(fib)
fib = count(fib)
在memo中,有些走到了original fib function,有些则走到了cache
counted_fib.call_count输出的是走到了original fib function的情况,由于cache的存在,不会重复路径fib.call_count输出的是memo的总次数
时间复杂度优化

从线性->对数复杂度:

Space
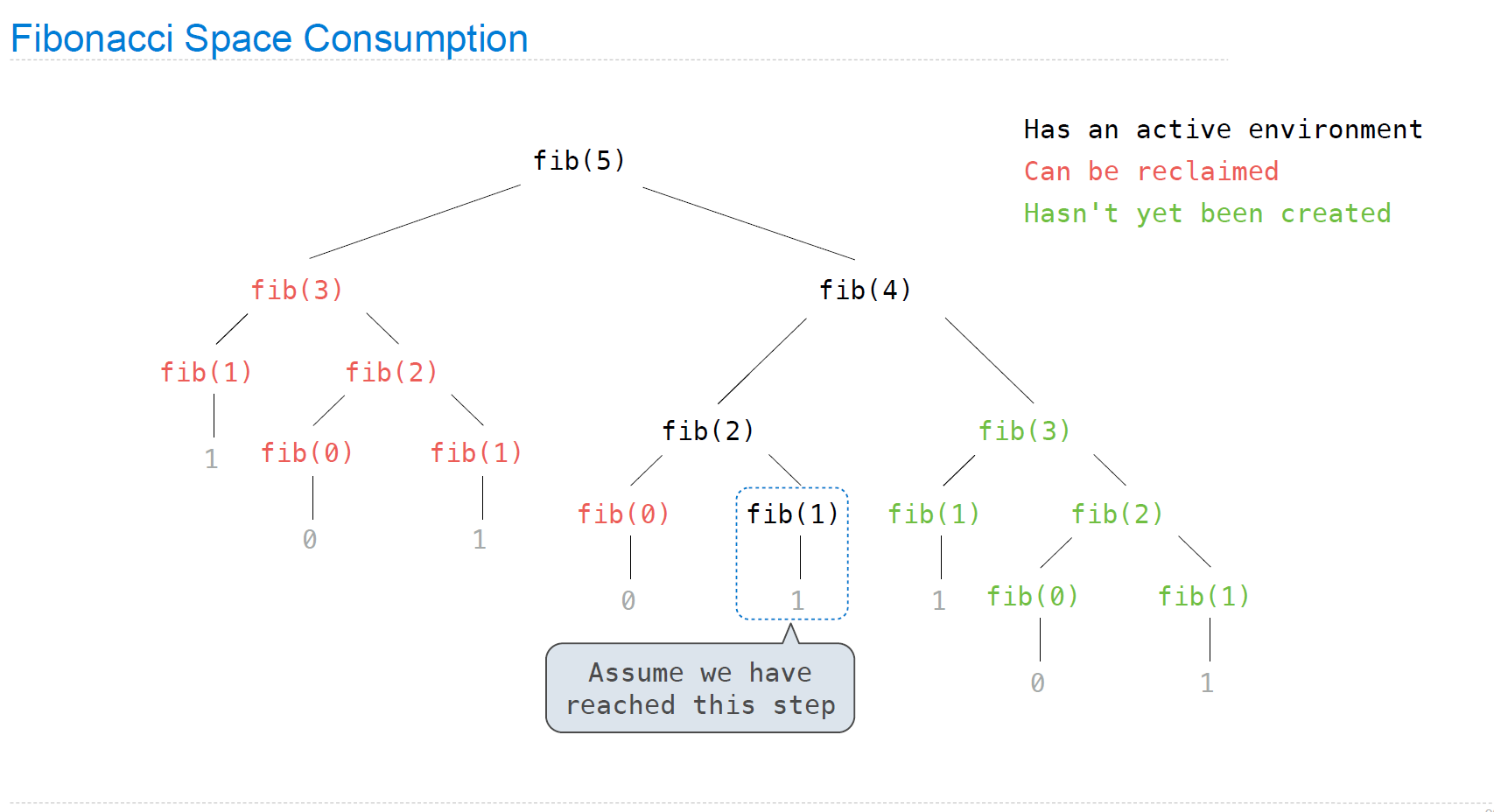
以fib为例,最大占用空间,或者说active environment是多少?
def count_frames(f):
"""Return a counted version of f with a max_count attribute."""
def counted(n):
counted.open_count += 1
counted.max_count = max(counted.max_count, counted.open_count)
result = f(n)
counted.open_count -= 1
return result
counted.open_count = 0
counted.max_count = 0
return counted
此时,counted.max_count应当为fib树的最长路径:
Lab 08 Optional Problem 1
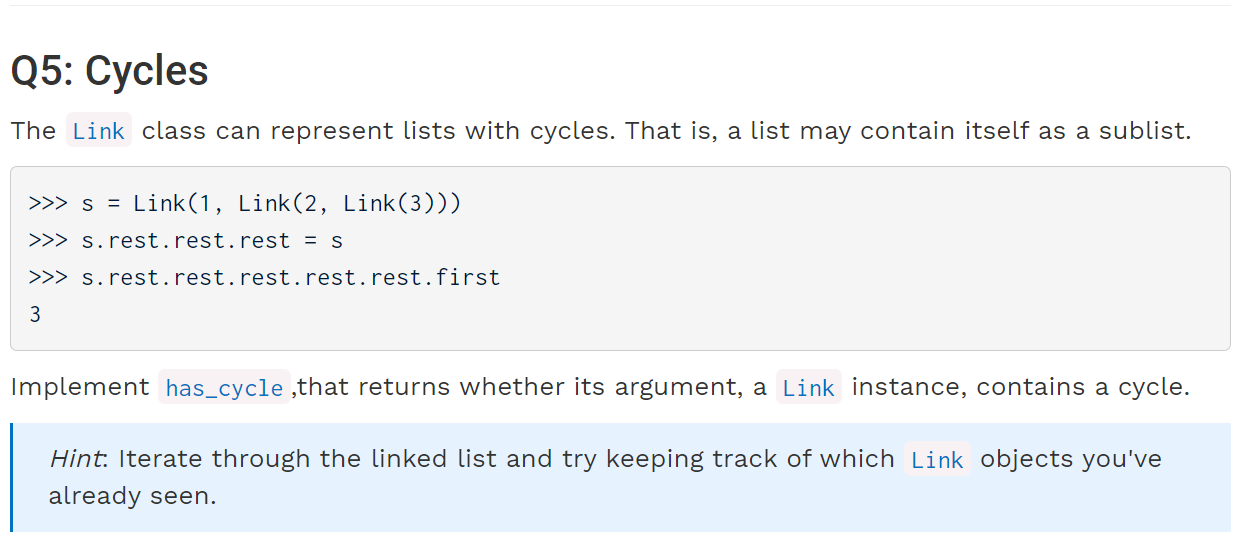
如果使用线性空间复杂度,我们可以把即将遍历的每一个s.rest都加入列表中,直到发现了重复的s.rest为止:
def has_cycle(link):
"""Return whether link contains a cycle."""
Link_lst = []
while link is not Link.empty:
# 其实这里比较的相当于是地址了
if link in Link_lst:
return True
Link_lst.append(link)
link = link.rest
return False
但是还有一种常数空间复杂度的实现方法,比较巧妙,思路是用两个指针同时遍历链表,一个指针走的一定要比另一指针快一步,这意味着两者一定会在某一点相遇,经过证明,相遇位置一定是链表的最后一位:

def has_cycle_constant(link):
"""Return whether link contains a cycle."""
slow, fast = link, link.rest
while fast is not Link.empty:
if fast.rest is Link.empty:
return False
# 如果slow已经与fast.rest相同,则不需要继续遍历了
if slow is fast or slow is fast.rest:
return True
slow, fast = slow.rest, fast.rest.rest
return False
Lab 08 (Trees & Linked Lists)
Mutate itself problem
Q4 (Tree)
这种类型的题目要求在原数据上进行修改,所以不可以返回任何值。
def cumulative_mul(t):
"""Mutates t so that each node's label becomes the product of all labels in
the corresponding subtree rooted at t."""
if t.is_leaf():
return
for b in t.branches:
cumulative_mul(b)
t.label *= b.label
在这里递归的作用仅仅是串联不同深度(或者前后位置),他不返回任何值,所以不可能出现类似于a=f(b)的递归赋值表达式,也不会出现在for循环中作为迭代器使用。
Q3 (Linked Lists)
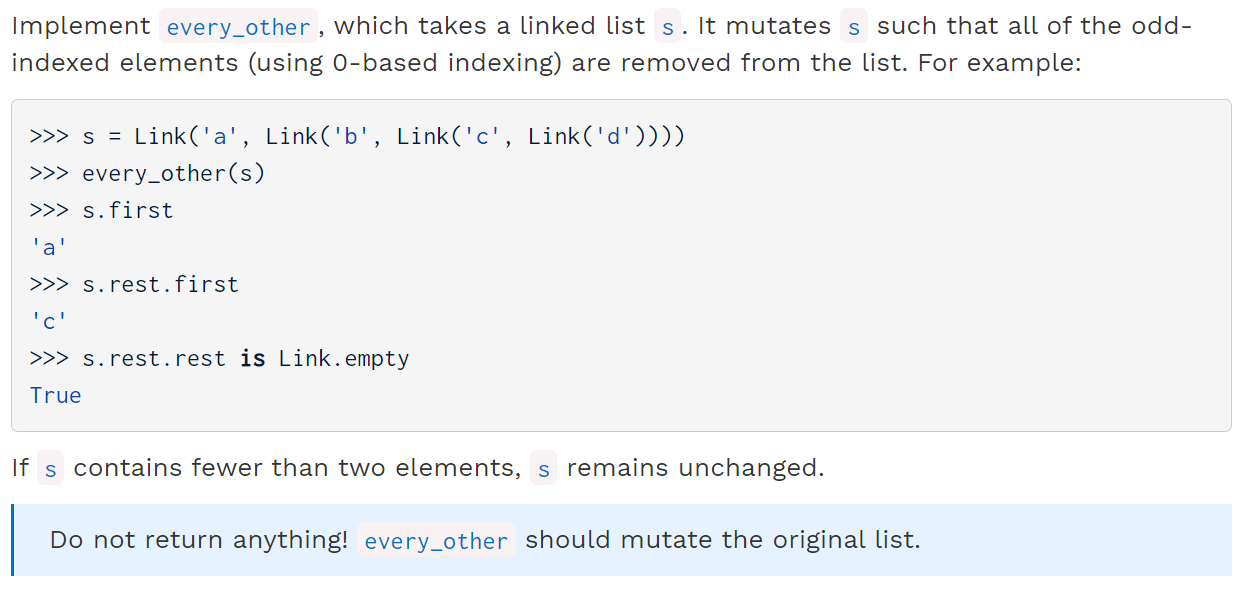
def every_other(s):
"""Mutates a linked list so that all the odd-indiced elements are removed
(using 0-based indexing)."""
if s is Link.empty or s.rest is Link.empty:
return
else:
s.rest = s.rest.rest
every_other(s.rest)
同样地,我们可以思考为什么在Q3中,递归部分放在对S操作之后,这是因为这里对link list的处理是从前往后的,而在Q4中对Tree的处理则是从叶结点逐渐上升到root的。
Mutation & Combination
def combine_mutate(lnk1,lnk2):
if lnk1 is Link.empty:
return lnk2
if lnk2 is Link.empty:
return lnk1
if lnk1.first <= lnk2.first:
s.rest = combine_mutate(lnk1.rest,lnk2)
return s
else:
t.rest = combine_mutate(lnk1,lnk2.rest)
return t
Every-other problem
处理此类问题有两种方法:
- 跟踪目前所在的深度或者位置
- 只处理需要处理的层(越过不需处理的位置)
上边的Q3就是采用了第二种方法,对于树,我们也可以进行类似的操作:
Optional Problem 2
def reverse_other(t):
"""Mutates the tree such that nodes on every other (odd-depth) level
have the labels of their branches all reversed."""
if t.is_leaf():
return
label_of_branches = [b.label for b in t.branches][::-1]
for i in range(len(label_of_branches)):
t.branches[i].label = label_of_branches[i]
# 越过偶数层
for b in t.branches[i].branches:
reverse_other(b)
disc 08

这道题目如果我们通过第一种方法实现,则可以设立helper函数追踪所在深度:
def alt_tree_map(t, map_fn):
def helper(t, depth):
if depth % 2 == 0:
label = map_fn(t.label)
else:
label = t.label
branches = [helper(b, depth + 1) for b in t.branches]
return Tree(label, branches)
return helper(t, 0)
Intersection Linked List Problem

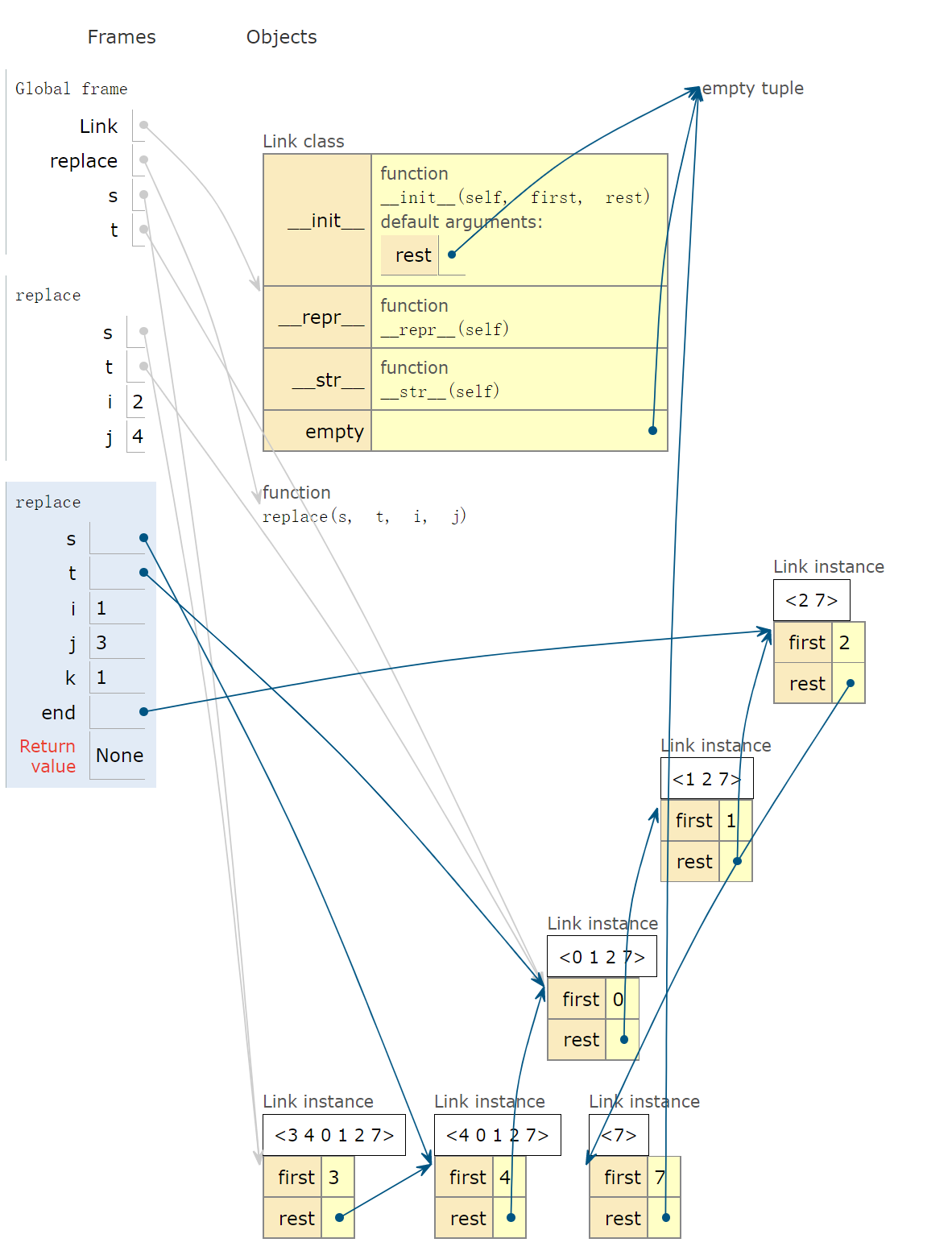
个人感觉这是一道有参考意义的链表操作题目,目的是将原链表中的某一段替换为新的链表元素
首先为了方便应用s.rest进行操作,我们先考虑把链表指针移动到i==1的位置,这样s.rest就直接对应着需要操作的部分,所以在i>1时应当使用递归:
if i > 1:
replace(s.rest,t,i-1,j-1)
接下来,我们应用lab 08 Q3中的操作技巧,将需要替换的链表段去除:
for _ in range(j-i):
s.rest = s.rest.rest
现在,要把t插入到当前的s.rest位置,同时把余下的s的元素插入到已经被连接到s的t的末尾,那么首先我们要找到t的末尾:
end = t
while end.rest is not Link.empty:
end = end.rest
之后做链接:
s.rest, end.rest = t, s.rest
environment diagram画出来是这样:
Combine Problem
在lab 05中,有一道类似的组合结构类题目,使用zip函数将两棵树合并在一起,我们可以将拿到题目用更普遍的形式写出来:

def combine_tree(t1,t2,combiner):
return Tree(combiner(t1.label,t2.label),[combine_tree(b1,b2,combiner) for b1,b2 in zip(t1.branches,t2.branches)])
同样地,面对lined lists时我们也会遇到这种组合类问题,比如:

因为本题中链表的数目不定,所以不太方便使用zip函数,能想到的方法是要遍历lst_of_lnks:
def multiply_lnks(lst_of_lnks):
product = 1
for lnk in lst_of_lnks:
if lnk is Link.empty:
return Link.empty
为了同时遍历多个链表,我们首先要把多个链表的头部元素全部处理完,之后建立一个全部为link.rest的链表并递归:
def multiply_lnks(lst_of_lnks):
product = 1
for lnk in lst_of_lnks:
if lnk is Link.empty:
return Link.empty
product *= lnk.first
lst_of_lnk_rest = [lnk.rest for lnk in lst_of_lnks]
return Link(product,multiply_lnks(lst_of_lnk_rest))
Find-Paths Problem
之前的相关例子:
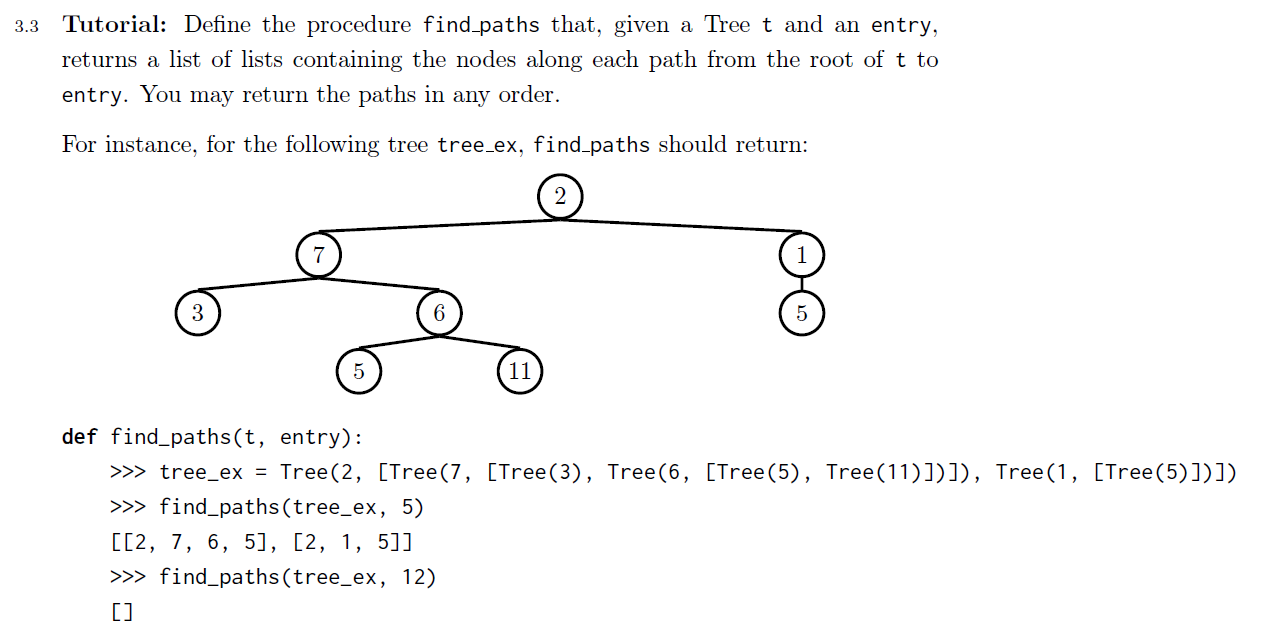
这道题与disc 05不同之处在于,树中可能存在多条符合题意的路径,这意味着我们没法使用前序遍历二叉树的方法,因为根节点需要出现在每一个符合题意的路径最前端,所以我们需要在每一次循环中都把当前的根节点加上,设立一个paths数组完成此目标,首先考虑base case:
def find_paths(t,entry):
paths = []
if t.label == entry:
paths.append([t.label])
需要注意的是,这里的base case不可以直接返回[t.label],我们要把结果储存在paths中,最后返回paths
for b in t.branches:
# 考察branches下的多个路径:
for path in find_paths(b, entry):
# 对于每一个路径,都要加上根节点的值
paths.append([t.label] + path)
return paths
这道题目也为4的解法提供了新的思路
Matching Problem
fa18-mt2

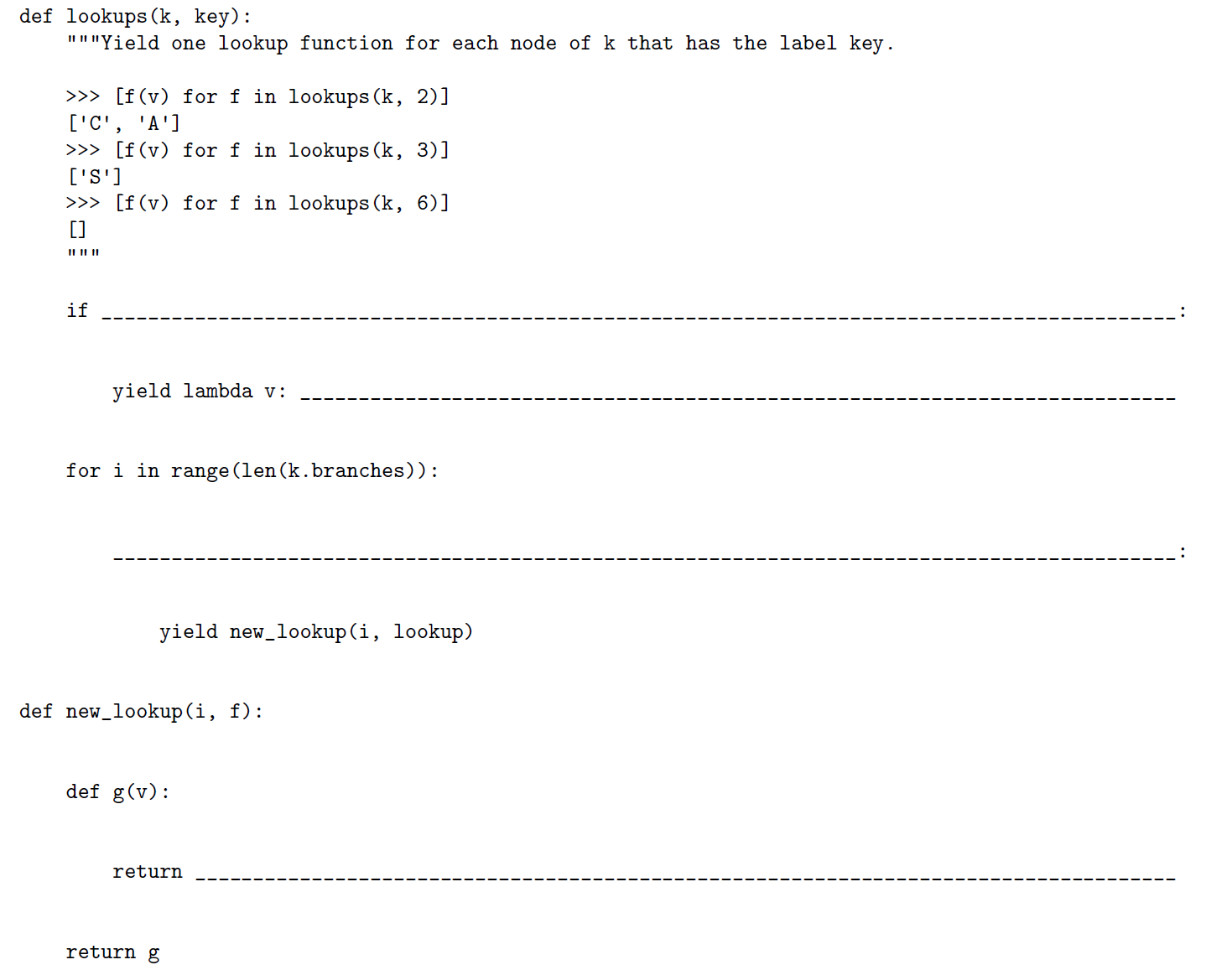
这道题目应当还有另一种做法:先通过zip函数把两个树组合起来,组合树的节点值为包含两个元素的列表,如此一来,可以通过搜索组合树节点值,来确定对应的字典值为多少。
题目中的做法是先处理一棵树,处理的关键部分在于函数lookups里for循环的部分,我们可以通过两条思路来填这个空:
- 考察寻找的值就位于根节点下边一层的情况(这个想法还可以帮助我们确定
new_lookup的内容) - 在一个分支中,还要继续寻找,直到找到对应的值为止,所以需要建立一个递归
def lookups(k,key):
if k.label == key:
yield lambda v: v.label
for i in range(len(k.branches)):
# 可以只考虑对应值位于根节点下边一层的情况
for lookup in lookups(k.branches[i], key):
yield new_lookup(i, lookup)
def new_lookup(i, f):
def g(v):
return f(v.branches[i])
return g
如果要完全验证该递归的正确性,我们会发现
lookups返回的是一个生成器,其中内容为new_lookup(i1,new_lookup(i2,...)),如此一来,当v作为参数给入时,就会持续被更新为v.branches[i1].branches[i2]...
Prune trees Problem
基本的裁剪问题的进化版

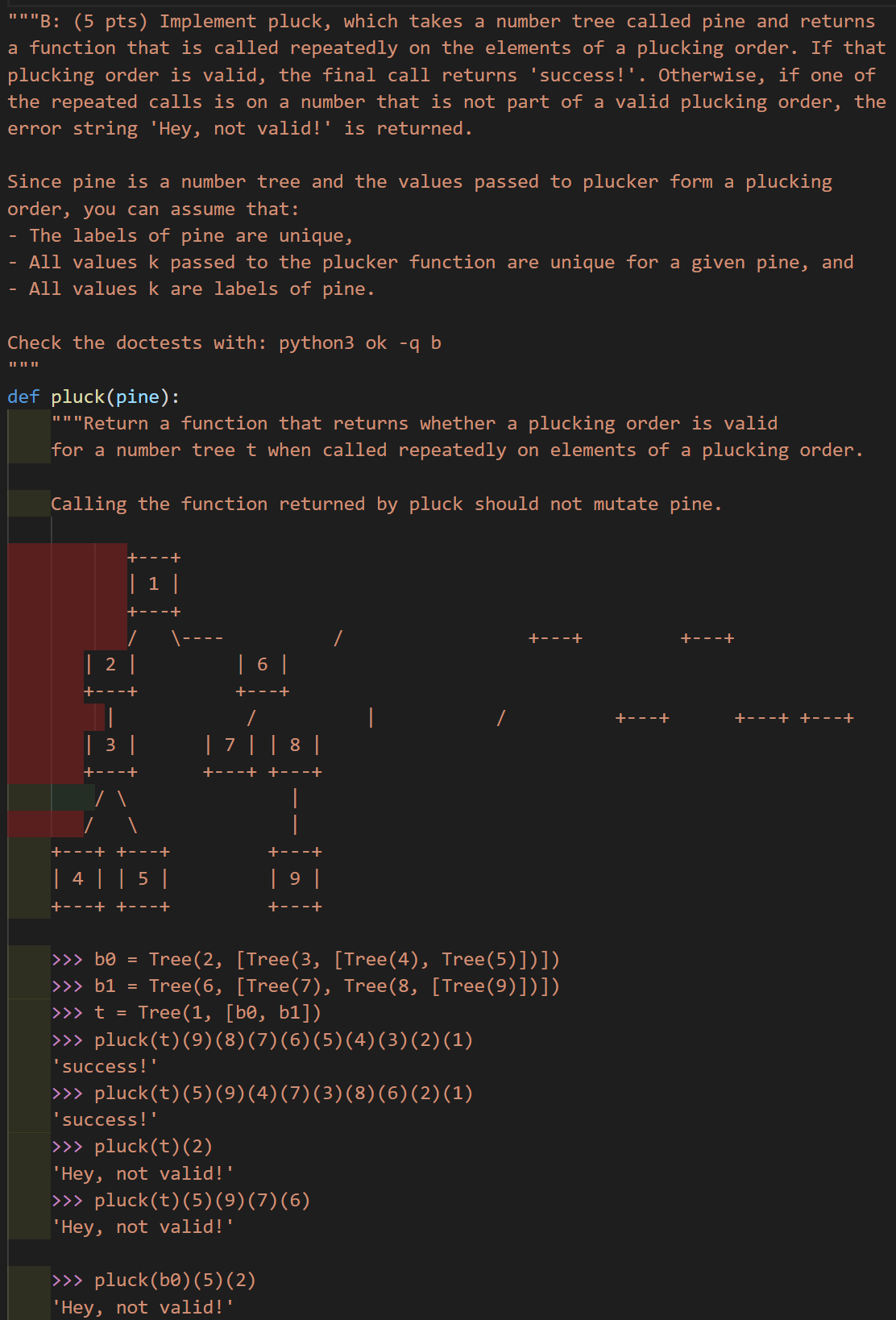
这题目好长……
def pluck(pine):
def plucker(k):
def pluck_one_leaf(cyprus):
"""Return a copy of cyprus without leaf k and check that k is a
leaf label, not an interior node label.
"""
# base case, it will not be a leaf
if cyprus.label == k:
return 'Hey, not valid!'
plucked_branches = []
for b in cyprus.branches:
# 跳过某个叶结点
skip_this_leaf = b.label == k and not b.branches
if not skip_this_leaf:
plucked_branch_or_error = pluck_one_leaf(b)
if isinstance(plucked_branch_or_error, str):
return plucked_branch_or_error
else:
plucked_branches += [plucked_branch_or_error]
return Tree(cyprus.label, plucked_branches)
nonlocal pine
if pine.is_leaf():
assert k == pine.label, 'all k must appear in pine'
return 'success!'
# 每次返回一个被裁剪之后的新树,到这一步的一定已经不是叶结点了
pine = pluck_one_leaf(pine)
if isinstance(pine, str):
return pine
return plucker
return plucker
注意到函数内部裁剪某个节点所使用的方法
F20 Lecture 23 (Modular Programming)
在教授给出的例子当中,使用如下方法构建restuarant列表+构建reviewers列表(主要参考其对json文件的操作流程)
def load_reviews(reviews_file):
reviewers_by_restaurant = {}
for line in open(reviews_file):
r = json.loads(line)
business_id = r['business_id']
if business_id not in reviewers_by_restaurant:
reviewers_by_restaurant[business_id] = []
reviewers_by_restaurant[business_id].append(r['user_id'])
return reviewers_by_restaurant
def load_restaurants(reviewers_by_restaurant, restaurants_file):
for line in open(restaurants_file):
b = json.loads(line)
reviewers = reviewers_by_restaurant.get(b['business_id'], [])
Restaurant(b['name'], b['stars'], sorted(reviewers))
load_restaurants(load_reviews('reviews.json'), 'restaurants.json')
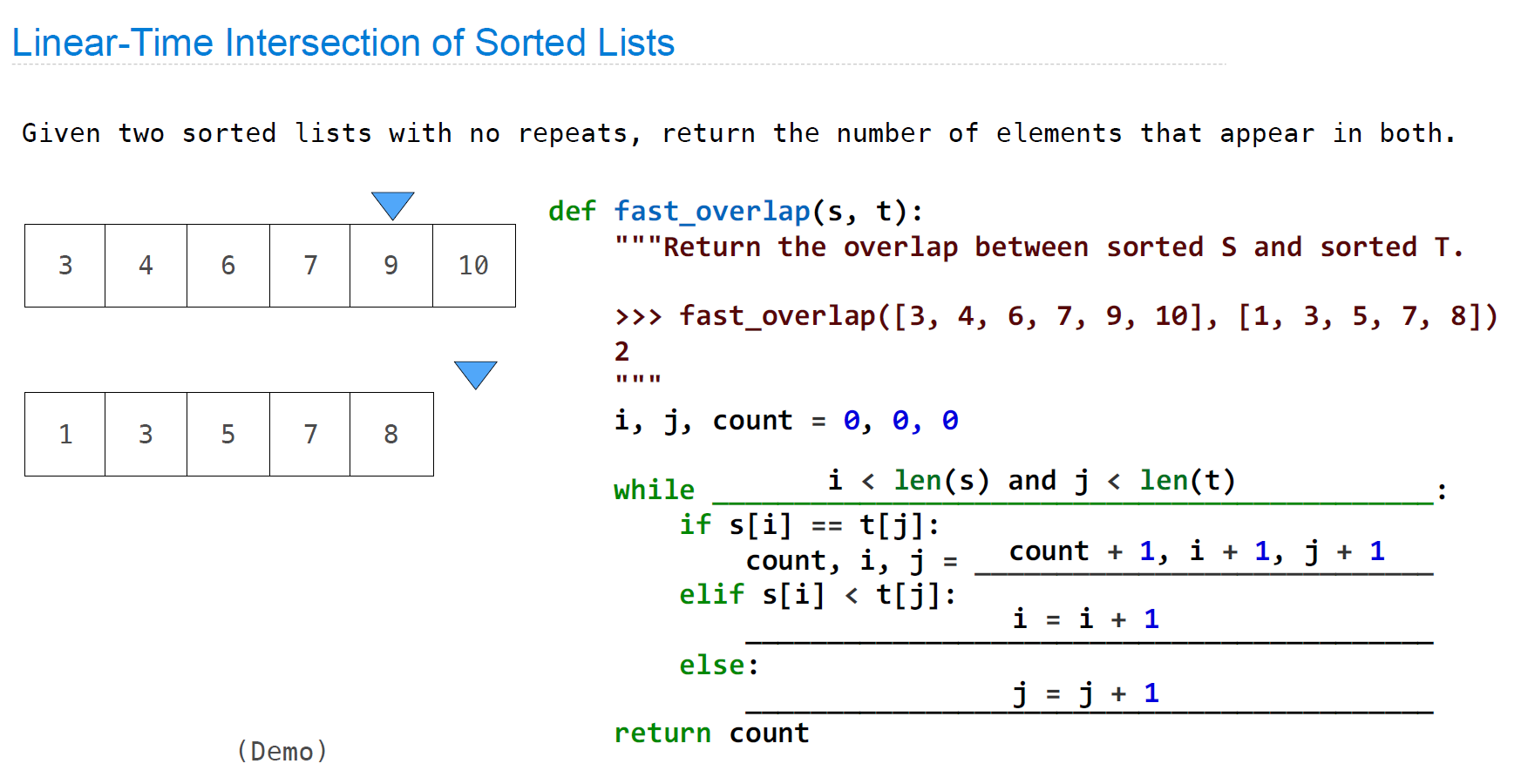
同时,案例中对similarity的考察函数进行了优化,将其从quadortic time变化为linear time,方法是对两个以及被排序好的列表使用两个指针同时遍历,并根据数据大小决定移动哪一个指针:
Linear time Intersection of Sorted Lists:
def fast_overlap(s, t):
"""Return the overlap between sorted S and sorted T."""
count, i, j = 0, 0, 0
while i < len(s) and j < len(t):
if s[i] == t[j]:
count, i, j = count + 1, i + 1, j + 1
elif s[i] < t[j]:
i += 1
else:
j += 1
return count
F20 Lecture 27 (Functional Programming)
Basic Definition
使用scheme语言进行函数式编程,基本的概念如下:
- Scheme Expressions

- Special Forms

这里的procedures也即functions
- Lambda Expressions
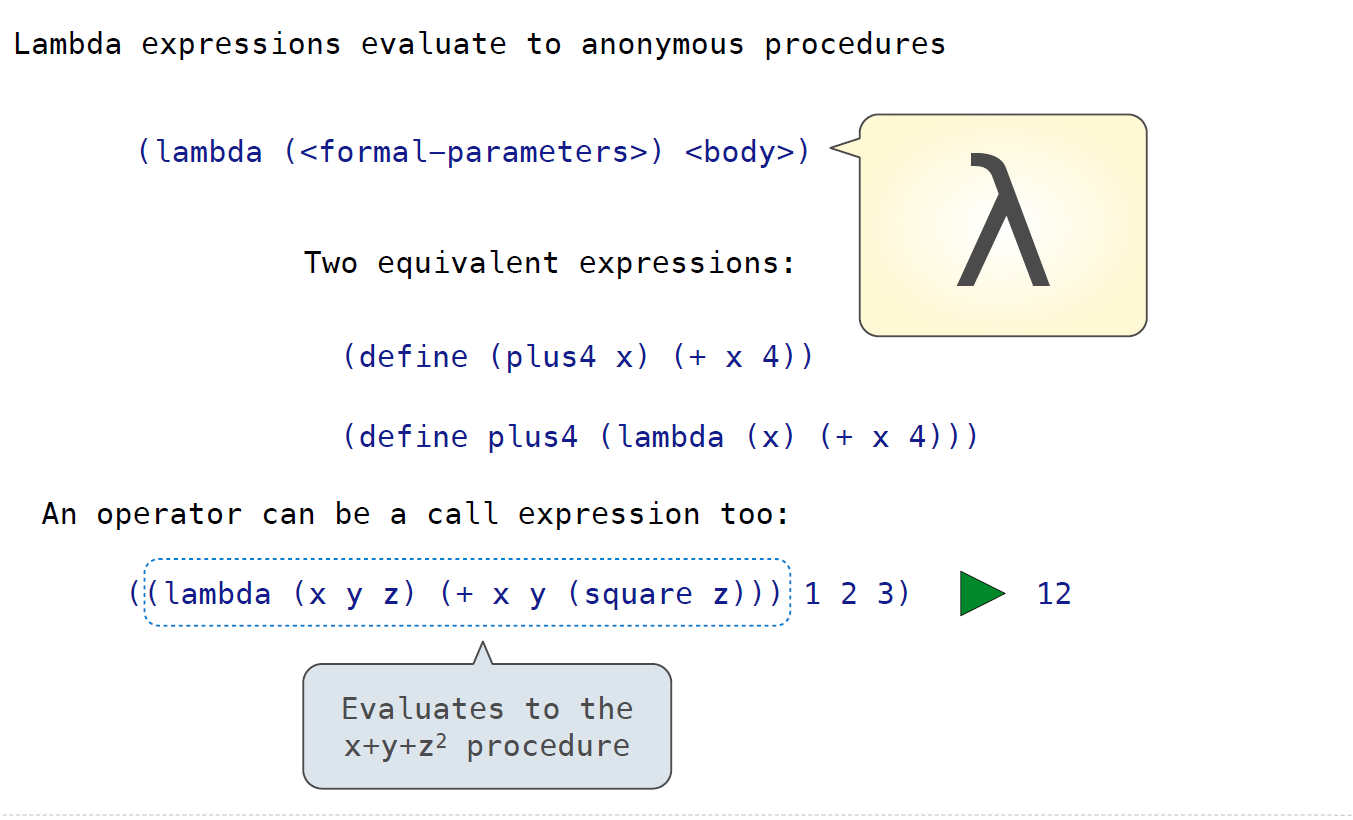
- More Special Forms
Let\cons\car\cdr\nil\cond\begin…
- Symbolic Programming

- Quasiquotation

(atom? 'a) #t
Interpreters
Parsing Expressions

包含词法分析与句法分析两部分:
- Lexical analysis: interprets a string as a token sequence is called a tokenizer or lexical analyzer
>>> tokenize_line('(+ 1 (* 2.3 45))')
['(', '+', 1, '(', '*', 2.3, 45, ')', ')']
- Syntactic analysis: The component that interprets a token sequence as an expression tree is called a syntactic analyzer. Syntactic analysis is a tree-recursive process, and it must consider an entire expression that may span multiple lines.
因为在句法分析时,要包含分析可能存在的subexpression,所以需要使用tree recursion
The
scheme_readfunction first checks for various base cases, including empty input (which raises an end-of-file exception, calledEOFErrorin Python) and primitive expressions. A recursive call toread_tailis invoked whenever a(token indicates the beginning of a list.The
read_tailfunction continues to read from the same inputsrc, but expects to be called after a list has begun. Its base cases are an empty input (an error) or a closing parenthesis that terminates the list. Its recursive call reads the first element of the list withscheme_read, reads the rest of the list withread_tail, and then returns a list represented as aPair.
# Scheme list parser, without quotation or dotted lists.
def scheme_read(src):
"""Read the next expression from src, a Buffer of tokens."""
if src.current() is None:
raise EOFError
val = src.pop()
if val == 'nil':
return nil
elif val not in DELIMITERS: # ( ) ' .
return val
elif val == "(":
# 开始一层括号的递归
return read_tail(src)
else:
raise SyntaxError("unexpected token: {0}".format(val))
def read_tail(src):
"""Return the remainder of a list in src, starting before an element or )."""
if src.current() is None:
raise SyntaxError("unexpected end of file")
if src.current() == ")":
src.pop()
return nil
# 只有又出现一层parenthesis时才会出现内层递归,否则是scheme_read的base case,返回val
# 如果在某一层递归内找到了')',则本层递归结束
first = scheme_read(src)
rest = read_tail(src)
return Pair(first, rest)
通过句法分析,将词法分析构成的token_list转化为Pair Object. 之后我们要根据scheme_list中的operator对operands采取适当的操作:
Evaluation & Apply
def scheme_eval(expr, env, _=None):
"""Evaluate Scheme expression EXPR in environment ENV."""
# Evaluate atoms
if scheme_symbolp(expr):
return env.lookup(expr)
elif self_evaluating(expr):
return expr
# All non-atomic expressions are lists (combinations)
if not scheme_listp(expr):
raise SchemeError('malformed list: {0}'.format(repl_str(expr)))
first, rest = expr.first, expr.rest
if scheme_symbolp(first) and first in SPECIAL_FORMS:
return SPECIAL_FORMS[first](rest, env)
else:
# 通过scheme_eval(first, env)将str转化为procedure,也就是函数,利用的是base case的返回值
operator1 = scheme_eval(first, env)
if isinstance(operator1, MacroProcedure):
return scheme_eval(operator1.apply_macro(rest, env), env)
validate_procedure(operator1)
arguments = rest.map(lambda x1: scheme_eval(x1, env))
return scheme_apply(operator1, arguments, env)
scheme_eval的设计接受嵌套形式的表达式,最后只需把已经计算过的子表达式传递给scheme_apply即可,需要注意的是,应对着三种不同的参数传入形式:primitive expressions、call expressions、special forms,只有call expressions会直接在scheme_eval内部继续递归,special_form的处理是交给scheme.py里的do_xx_form.
>>> def calc_apply(operator, args):
"""Apply the named operator to a list of args."""
if not isinstance(operator, str):
raise TypeError(str(operator) + ' is not a symbol')
if operator == '+':
return reduce(add, args, 0)
elif operator == '-':
if len(args) == 0:
raise TypeError(operator + ' requires at least 1 argument')
elif len(args) == 1:
return -args.first
else:
return reduce(sub, args.second, args.first)
elif operator == '*':
return reduce(mul, args, 1)
elif operator == '/':
if len(args) == 0:
raise TypeError(operator + ' requires at least 1 argument')
elif len(args) == 1:
return 1/args.first
else:
return reduce(truediv, args.second, args.first)
else:
raise TypeError(operator + ' is an unknown operator')
这里使用的是课程内容里calculator的calc_apply函数,因为更能直接地体现出该函数的作用,scheme_apply函数会在每次scheme_eval对call_expression评估完成后使用。scheme_apply的设计逻辑为:
- Apply happens in the
scheme_applyfunction. If the function is a built-in procedure,scheme_applycalls theapplymethod of thatBuiltInProcedureinstance. If the procedure is a user-defined procedure,scheme_applycreates a new call frame(在其中将参数与值绑定) and callseval_allon the body of the procedure, resulting in a mutually recursive eval-apply loop.
Read-eval-print-loops
通过REPL的方法,可以实现与interpreter的交互:
>>> def read_eval_print_loop():
"""Run a read-eval-print loop for calculator."""
while True:
try:
src = buffer_input()
while src.more_on_line:
expression = scheme_read(src)
print(calc_eval(expression))
except (SyntaxError, TypeError, ValueError, ZeroDivisionError) as err:
print(type(err).__name__ + ':', err)
except (KeyboardInterrupt, EOFError): # <Control>-D, etc.
print('Calculation completed.')
return
如果我们将上述几个基本步骤拓展到scheme interpreter的实现中,参见详细的文档描述:
http://composingprograms.com/pages/35-interpreters-for-languages-with-abstraction.html
关于scheme中的lambda
lambda为scheme中的一些其他的special form提供了方法,比如define user-defined procedures:
scm> (define f (lambda (x) (* x 2)))
f
; 简写的形式即为:
scm> (define (f x) (* x 2))
同时,对于let,也可以使用lambda进行转化,这是scheme interpreter项目中的一个问题,摘出一部分:
((let? expr)
(let ((values (cadr expr))
(body (cddr expr)))
(append (cons (cons 'lambda (cons (car (zip values)) (map let-to-lambda body))) nil) (map let-to-lambda (cadr (zip values))))
))
需要注意的是,在scheme中处理递归问题的一个常用手法是使用map函数,这允许我们处理嵌套的子表达式。而因为let带有的表达式中可能存在好几个子list,所最后要将他们append在一起。形成如下的效果:
scm> (let-to-lambda '(let ((a 1) (b 2)) (+ a b)))
((lambda (a b) (+ a b)) 1 2)
scm> (let-to-lambda '(let ((a 1)) (let ((b a)) b)))
((lambda (a) ((lambda (b) b) a)) 1)
map
关于scheme中map的使用,这里还有几个例子:
- 设计
scheme中的zip函数:
(define (zip lst)
(if (= 1 (length (car lst)))
(cons (map car lst) nil) (cons (map car lst) (zip (map cdr lst)))
)
)
- Fall 2019 final Q7

其中,(b)的解法可以这样理解:首先思考函数的功能,从抽象层面思考代码实现:mul-expr的功能是将所有的sub-expression或者primitive expression乘起来,而为了达到此目标,我们需要将每一个子表达式全部映射为(转化为)值,再将这些值相乘得到最后的结果 – 可以通过map函数的方法实现:
(if (number? e) e
(mul (map mul-expr (cdr e))))
在有了(b)的基础之后,c其实是一样的思路,最终的效果应该如下:
(*-to-mul '(* 1 2 (* 3 4)))->(mul (list 1 2 (mul (list 3 4))))
所以,当我们遇到*时,就应当立刻把*替换为mul,同时在它的sub-expression上应用(b)的map进行下一层递归。而当符号不是*时,我们只需要返回原来的表达式即可,并不需要其他多余的操作。
个人感觉这样写更清楚一些:
(define (*-to-mul e)
(if (not (list? e))e
(let ((op (car e)) (rest (cdr e))
(if (equal? op '*)
(list 'mul (cons 'list (map *-to-mul rest)))
(cons op rest))))))
Tree recursion在scheme中的应用
Project Scheme Q17
在之前的Parsing Expressions部分,在做句法分析时,设计了scheme_read和read_tail函数,并通过mutual recursion的方法进行了一个tree recursion的过程,现在我们可以将这种思路直接运用到scheme语言中:
Define a function nondecreaselist, which takes in a scheme list of numbers and outputs a list of lists, which overall has the same numbers in the same order, but grouped into lists that are non-decreasing.
For example, if the input is a list containing elements
(1 2 3 4 1 2 3 4 1 1 1 2 1 1 0 4 3 2 1)
the output should contain elements
((1 2 3 4) (1 2 3 4) (1 1 1 2) (1 1) (0 4) (3) (2) (1))
(define (nondecreaselist s)
(cond ((null? s) nil)
((> (car s) (car (cdr s))) (cons (cons (car s) nil) (nondecreaselist (cdr s))))
(else (cons (cons (car s) (car (nondecreaselist (cdr s)))) (cdr (nondecreaselist (cdr s)))))
)
)
注意到实现中,如果前一个元素的值大于后一个元素,则此时括号闭合,没有在本层括号体内发生递归,类似于前边的scheme_read情况;否则,将会在本层括号内部发生递归,但是我们必须确保下一层递归出来的第一个元素在括号内(因为已经被排序);则括号外部需要从列表第二个元素开始排起,并最终连接成完整列表,有点类似于read_tail的想法。在这里,因为是函数式编程,我们更不需要去追溯函数的遍历过程,从抽象的角度考虑,当已经检测的两个元素确定可以放在同一个括号内部时,需要在括号内部与括号外部同时进行递归,同时,我们利用car与cdr确保已经经过比较的元素在应有的位置。
F20 Lecture 33 Q & A

这道题我们采用不利用helper函数的方法来解,要比答案中的方法简单许多,因为我们只需要先讨论(car lst)是否为list,其后在讨论是否满足filter-fn的条件即可:
(define (skip-list lst filter-fn)
(cond ((null? lst) nil)
((list? (car lst)) (append (skip-list (car lst) filter-fn) (skip-list (cdr lst) filter-fn)))
(else (if (filter-fn (car lst))
(cons (car lst) (skip-list (cdr lst) filter-fn))
(skip-list (cdr lst) filter-fn)
)
)
)
)
需要注意的是,在第二个条件判断时连接列表时,我们需要使用append而不是cons,这是因为在两个元素均为list的情况下,如果使用cons将会产生nested lists的效果,多出几层括号。
Tail Call Optimization
在最后的大项目的optional problem中,遇到了尾调用的优化问题,在这里浅显的总结一下:
- 什么是尾递归?
尾递归,比线性递归多一个参数,这个参数是上一次调用函数得到的结果; 所以,关键点在于,尾递归每次调用都在收集结果,避免了线性递归不收集结果只能依次展开消耗内存的坏处
可以通过几个例子来证明:
(define (sum n total)
(if (zero? n) total
(sum (- n 1) (+ n total))))
(sum 1001 0)
在这里,total就是被我们用来保存调用函数结果的参数,更纤细点说,这样做可以在上层函数执行结束后销毁堆栈,因为我们已经不需要了,所有的对后续处理有用的结果被我们保存在total中。
- 实现尾递归优化的方法
在本项目中,方法是使用一个Thunk,简单来说就是收集结果,在下次需要调用时使用。
The
Thunkclass represents a thunk, an expression that needs to be evaluated in an environment. Whenscheme_optimized_evalreceives a non-atomic expression in atailcontext, then it returns anThunkinstance. Otherwise, it should repeatedly callprior_eval_functionuntil the result is a value, rather than aThunk.
我们需要判断在scheme代码中,那些可能的位置会出现tail recursive的情况:比如or的末尾、and的末尾、if的末尾、begin的末尾(在eval_all里)等等。当在这些位置上进行tail call时,我们就返回Thunk,其中包含着当前的frame。之后通过对Thunk.expr的调用,即可继续进行新一轮的递归。而如果不在末位,本轮递归的frame还需要继续存在,所以不能直接返回Thunk。

通过几个例子来说明一下:

在上边一个例子里,第一个if就不是tail context,什么是tail context?不仅仅是最后一个evaluate的部分,而是说通过在最后evaluate该部分,可以返回得到当前的procedure的计算结果,在当前部分的environment frame来继续剩余操作了。显然这里的if不符合。
在第二个例子中,第一个红色部分也不是tail context,因为他不处于最后的位置,同时其中的小红圈也不是tail call,因为evaluate该call expression不能得到整体的返回结果,environment frame同样无法被丢弃,前边还有(+ current)。
实现map & reduce
- 关于
reduce的实现:recursive call is a tail call:
(define (reduce procedure s start)
(if (null? s) start
(reduce procedure
(cdr s)
; change the start
(procedure (car s) start))
)
)
- 两种
map的实现方法:
- 非尾递归:
(define (map procedure s)
(if (null? s) nil
(cons (procedure (car s)) (map procedure (cdr s)))
)
)
因为最后map的返回值还要用来组成cons,所以这里是一个tail context,但并非tail call.
- 尾递归:
(define (map procedure s)
(define (map-reverse s m)
(if (null? s) m)
(map-reverse (cdr s) (cons (procedure (car s)) m)))
)
)
(reverse (map-reverse s nil))
)
注意到这里的实现方法是一个典型的tail recursion的方法,在函数参数中增添一个用以存储当前计算结果,当数据全部执行完毕后,返回该参数。
(define (reverse s)
(define (reverse-iter s r)
(if (null? s)
r
(reverse-iter (cdr s)
(cons (car s) r))))
(reverse-iter s nil))
Macro
在scheme语言中,我们通过调用define-macro使用内部定义的macro函数。macro的执行方法与一般的procedure不一样,总的来说需要经过三个步骤:

首先第一步,evaluate在call expression中的operator部分,也即twice,之后在返回的macro中调用operand expression绑定,但不去evaluate the operand expression,而是在之前的工作全部结束后,evaluate the entire expression (body)。
为什么宏函数不可以这样写?
(define-macro (twice expr) (begin expr expr))因为在执行第二步时,会先
call the macro procedure on the operand procedure,此时begin就会被eval
举个例子,我们可以写这样一个函数,用以评估x是否满足某条件,如果满足,则输出passed,如果不满足,则输出failed: ,以及不满足的条件。
使用macro可以这样定义:
(define-macro (check expr)
(list 'if expr ''passed (list 'quote (list 'failed: expr))))
; test
(define x -2)
(check (> x 0))
在执行时,注意每次evaluate call expression会去掉位于同一层的quote符号(位于'内部的'不会被展开),得到如下表达式:
(if (> x 0) 'passed (quote (failed: (> x 0) ) ) )
scheme_eval the above expression, then we get:
(failed: (> x 0))
上述操作是通过
define无法完成的,直接使用define会先计算(> x 0)
同样地,我们可以使用macro写出scheme中的for:
(define-macro (for sym vals expr) (list 'map (list 'lambda (list sym) expr) vals) )
scm> (for x '(2 3 4 5) (* x x))
(4 9 16 25)
Macro实现
在实际实现时,分成两个部分,在do_define_macro内部,我们可以依据do_define_form,稍作改动,因为不会出现define_macro x '(1 2)的这种形式,也就是说不能直接对symbol做绑定。
在scheme_eval中,按照之前描述执行过程的顺序,我们可以在判定operator对应的类型为MacroProcedure后,先利用apply_macro将实际的args与formals绑定(同时执行了call the Macro on the operand procedure,因为是一个mutual recursive的过程),在外边套一层scheme_eval,用以计算整体的最终结果。